Уравнение двухфакторной множественной регрессии

Двухфакторная линейная регрессия имеет вид: y=b₀+b₁x₁+b₂x₂

Назначение сервиса. Данный онлайн-калькулятор позволяет вычислить следующие показатели:

уравнение множественной регрессии через формулы Крамера;
матрицу парных коэффициентов корреляции;
уравнение регрессии в стандартизированном масштабе;
средние коэффициенты эластичности для множественной регрессии;
доверительные интервалы для индивидуального и среднего значения результативного признака;
множественный коэффициент детерминации, частные критерии F_x1 и F_x2;

В расчетах используется метод наименьших квадратов (МНК). Кроме него, при вычислении параметров уравнения множественной регрессии также можно воспользоваться матричным методом. Результат оформляется в отчете формата Word. Дополнительно создается шаблон построения множественной регрессии в Excel.
Кроме этого проводится проверка наличия предпосылок МНК:

Первая предпосылка МНК – случайный характер остатков ε_i.;
Вторая предпосылка МНК – нулевая средняя величина остатков, не зависящая от ε_i.;
Третья предпосылка МНК - дисперсия остатков должна была гомоскедастичной.;
Четвертая предпосылки МНК – отсутствие автокорреляции остатков.;
Пятая предпосылка МНК - нормальное распределение остатков.;

В многофакторных моделях результативный признак зависит от нескольких факторов. Множественный или многофакторный корреляционно-регрессионный анализ решает три задачи:

определяет форму связи результативного признака с факторными;
выявляет тесноту этой связи;
устанавливает влияние отдельных факторов.

Пример. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника Y (тыс. руб.) от ввода в действие новых основных фондов x₁(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x₂(%).
Требуется:

Построить линейную модель множественной регрессии. Записать стандартизированное уравнение множественной регрессии. На основе стандартизированных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Найти скорректированный коэффициенты парной, частной и множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
С помощью F- критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации R².
С помощью частных F- критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x₁ после x₂ и фактора x₂ после x₁.
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Исходные данные (таблица)

Номер предприятия	y	x₁	x₂
1	7	3,5	9
2	7	3,6	10
3	7	3,9	12
4	7	4,1	17
5	8	4,2	18
6	8	4,5	19
7	9	5,3	19
8	9	5,5	20
9	10	5,6	21
10	10	6,1	21
11	10	6,3	22
12	10	6,5	22
13	11	7,2	24
14	12	7,5	25
15	12	7,9	27
16	13	8,2	30
17	13	8,4	31
18	14	8,6	33
19	14	9,5	35
20	15	9,6	36

Решение.
1. Построить линейную модель множественной регрессии. Записать стандартизированное уравнение множественной регрессии. На основе стандартизированных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
Система трех линейных уравнений с тремя неизвестными b₀, b₁, b₂:
∑y_i = nb₀ + b₁∑x_1i + b₂∑x_2i
∑x_1iy_i = b₀∑x_1i + b₁∑x_1i² + b₂∑x_1ix_2i
∑x_2iy_i = b₀∑x_2i + b₁∑x_1ix_2i + b₂∑x_2i²

Y	X₁	X₂	X₁²	X₂²	X₁Y	X₂Y	X₁X₂	Y²
7	3.5	9	12.25	81	24.5	63	31.5	49
7	3.6	10	12.96	100	25.2	70	36	49
7	3.9	12	15.21	144	27.3	84	46.8	49
7	4.1	17	16.81	289	28.7	119	69.7	49
8	4.2	18	17.64	324	33.6	144	75.6	64
8	4.5	19	20.25	361	36	152	85.5	64
9	5.3	19	28.09	361	47.7	171	100.7	81
9	5.5	20	30.25	400	49.5	180	110	81
10	5.6	21	31.36	441	56	210	117.6	100
10	6.1	21	37.21	441	61	210	128.1	100
10	6.3	22	39.69	484	63	220	138.6	100
10	6.5	22	42.25	484	65	220	143	100
11	7.2	24	51.84	576	79.2	264	172.8	121
12	7.5	25	56.25	625	90	300	187.5	144
12	7.9	27	62.41	729	94.8	324	213.3	144
13	8.2	30	67.24	900	106.6	390	246	169
13	8.4	31	70.56	961	109.2	403	260.4	169
14	8.6	33	73.96	1089	120.4	462	283.8	196
14	9.5	35	90.25	1225	133	490	332.5	196
15	9.6	36	92.16	1296	144	540	345.6	225
206	126	451	868.64	11311	1394.7	5016	3125	2250
10.3	6.3	22.55	43.43	565.55	69.74	250.8	156.25	112.5

Для наших данных система уравнений имеет вид:
206 = 20 b₀ + 126b₁ + 451b₂
1394.7 = 126b₀ + 868.64b₁ + 3125b₂
5016 = 451b₀ + 3125b₁ + 11311b₂

Решая систему методом Крамера, находим:
b₀ = 2.212; b₁ = 1.099; b₂ = 0.0515
Уравнение регрессии: Y = 2.212 + 1.099 X₁ + 0.0515 X₂
Расчет β-коэффициентов можно выполнить и по формулам:

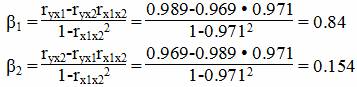
Стандартизированная форма уравнения регрессии имеет вид:
y⁰ = 0.84x₁ + 0.154x₂
Частные коэффициенты эластичности.
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:

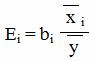
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора х_j на 1% от своего среднего уровня при фиксированном положении других факторов модели.

Частный коэффициент эластичности |E₁| < 1. Следовательно, его влияние на результативный признак Y незначительно.

Частный коэффициент эластичности |E₂| < 1. Следовательно, его влияние на результативный признак Y незначительно.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
Для расчета составим следующую таблицу:

Y	X₁	X₂	(Y_i-Y)²	(X_1i-X₁)²	(X_2i-X₂)²	(Y_i-Y)(X_1i-X₁)	(Y_i-Y)(X_2i-X₂)	(X_1i-X₁)(X_2i-X₂)
7	3.5	9	10.89	7.84	183.6	9.24	44.72	37.94
7	3.6	10	10.89	7.29	157.5	8.91	41.42	33.89
7	3.9	12	10.89	5.76	111.3	7.92	34.82	25.32
7	4.1	17	10.89	4.84	30.8	7.26	18.32	12.21
8	4.2	18	5.29	4.41	20.7	4.83	10.47	9.56
8	4.5	19	5.29	3.24	12.6	4.14	8.17	6.39
9	5.3	19	1.69	1	12.6	1.3	4.62	3.55
9	5.5	20	1.69	0.64	6.5	1.04	3.32	2.04
10	5.6	21	0.09	0.49	2.4	0.21	0.47	1.09
10	6.1	21	0.09	0.04	2.4	0.06	0.47	0.31
10	6.3	22	0.09	0	0.3	0	0.17	0
10	6.5	22	0.09	0.04	0.3	-0.06	0.17	-0.11
11	7.2	24	0.49	0.81	2.1	0.63	1.02	1.31
12	7.5	25	2.89	1.44	6	2.04	4.17	2.94
12	7.9	27	2.89	2.56	19.8	2.72	7.57	7.12
13	8.2	30	7.29	3.61	55.5	5.13	20.12	14.16
13	8.4	31	7.29	4.41	71.4	5.67	22.82	17.75
14	8.6	33	13.69	5.29	109.2	8.51	38.67	24.04
14	9.5	35	13.69	10.24	155	11.84	46.07	39.84
15	9.6	36	22.09	10.89	180.9	15.51	63.22	44.39
206	126	451	128.2	74.84	1140.95	96.9	370.7	283.7
10.3	6.3	22.55	6.41	3.74	57.05	4.85	18.54	14.19

Для y и x₁
Средние значения

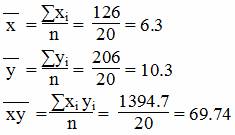
Дисперсия

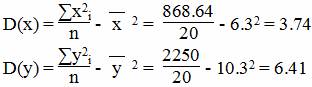
Среднеквадратическое отклонение

Коэффициент корреляции

Для y и x₂
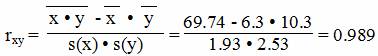
Средние значения

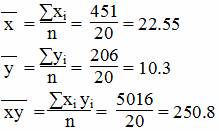
Дисперсия

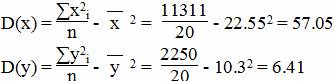
Среднеквадратическое отклонение

Коэффициент корреляции

Для x₁ и x₂
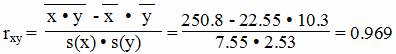
Средние значения

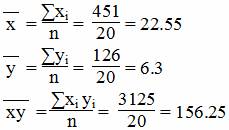
Дисперсия

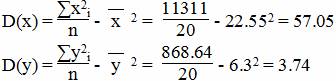
Среднеквадратическое отклонение

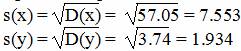
Коэффициент корреляции

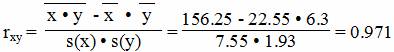
Матрица парных коэффициентов корреляции.

-	y	x₁	x₂
y	1	0.989	0.969
x₁	0.989	1	0.971
x₂	0.969	0.971	1

Коэффициенты регрессии b_i можно также найти по следующим формулам:

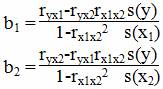
где r_yx1, r_yx2, r_x1x2 - коэффициенты парной корреляции между результатом и каждым из факторов и между факторами; s(x₁), s(x₂) - среднее квадратическое отклонение 1-го и 2-го факторов соответственно; s(y) - среднее квадратическое отклонение результативного признака.
Параметр a можно определить по формуле:

Наибольшее влияние на результативный признак оказывает фактор x₁ (r = 0.99), значит, при построении модели он войдет в регрессионное уравнение первым.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.

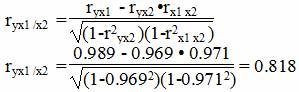
Теснота связи сильная

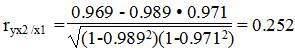
Теснота связи низкая.

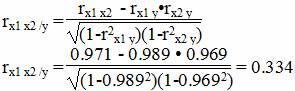
Теснота связи не сильная

Множественный коэффициент корреляции.
Расчёт коэффициента корреляции выполним, используя известные значения линейных коэффициентов парной корреляции и β-коэффициентов.

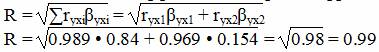
Коэффициент множественной корреляции определить через матрицу парных коэффициентов корреляции:

где Δ_r - определитель матрицы парных коэффициентов корреляции; Δ_r11 - определитель матрицы межфакторной корреляции.

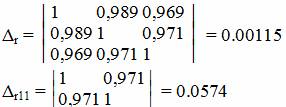
Коэффициент множественной корреляции

Аналогичный результат получим при использовании других формул:

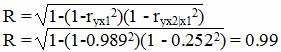
Связь между признаком Y и факторами X_i низкая.
Коэффициент детерминации: R² = 0.98
Таким образом, наибольшее влияние на результат оказывает x₁ (β=0,84 > 0,154; E = 0,67 > 0,11).

3. Найти скорректированный коэффициенты парной, частной и множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
Более объективной оценкой является скорректированный коэффициент детерминации:

Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.

4. С помощью F- критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации R² (проверим значимость совместной объясняющей способности всех независимых факторов модели).
Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y.
Проверим гипотезу об общей значимости - гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:
H₀: R² = 0; β₁ = β₂ = ... = β_m = 0.
H₁: R² ≠ 0.
Проверка этой гипотезы осуществляется с помощью F-статистики распределения Фишера (правосторонняя проверка).
Если F < F_kp = F_{α ; n-m-1}, то нет оснований для отклонения гипотезы H₀.

Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 20 - 2 - 1 = 17, Fkp(2;17) = 3.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно

5. С помощью частных F- критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1.
Частные критерии F_x1 и F_x2 оценивают статистическую значимость включения факторов x₁ и x₂ в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. F_x1 оценивает целесообразность включения в уравнение x₁ после включения в него фактора x₂.
Соответственно F_x2 указывает на целесообразность включения в модель фактора x2 после включения фактора x₁.

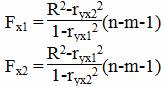
Найдем r_yx2¹, r_yx2².
r_yx1² = 0.989² = 0.979
r_yx2² = 0.969² = 0.939

Поскольку фактическое значение F > Fkp, то коэффициент F_x1 статистически значим, т.е. целесообразно включать в уравнение x₁ после включения в него фактора x₂. Прирост факторной дисперсии за счет дополнительного фактора x₁ является существенным.

Поскольку фактическое значение F < Fkp, то коэффициент F_x2 статистически не значим, т.е. не целесообразно включать в уравнение x₂ после включения в него фактора x₁.

6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
Значащий фактор x₁. Строим уравнение парной регрессии y = bx₁ + b₀.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

x	y	x²	y²	x·y
3.5	7	12.25	49	24.5
3.6	7	12.96	49	25.2
3.9	7	15.21	49	27.3
4.1	7	16.81	49	28.7
4.2	8	17.64	64	33.6
4.5	8	20.25	64	36
5.3	9	28.09	81	47.7
5.5	9	30.25	81	49.5
5.6	10	31.36	100	56
6.1	10	37.21	100	61
6.3	10	39.69	100	63
6.5	10	42.25	100	65
7.2	11	51.84	121	79.2
7.5	12	56.25	144	90
7.9	12	62.41	144	94.8
8.2	13	67.24	169	106.6
8.4	13	70.56	169	109.2
8.6	14	73.96	196	120.4
9.5	14	90.25	196	133
9.6	15	92.16	225	144
126	206	868.64	2250	1394.7

Для наших данных система уравнений имеет вид
20a + 126 b = 206
126 a + 868.64 b = 1394.7

Домножим уравнение (1) системы на (-6.3), получим систему, которую решим методом алгебраического сложения.
-126a -793.8 b = -1297.8
126 a + 868.64 b = 1394.7
Получаем:
74.84 b = 96.9
Откуда b = 1.2948
Теперь найдем коэффициент «a» из уравнения (1):
20a + 126·b = 206
20a + 126·1.2948 = 206
20a = 42.86
a = 2.143
Получаем эмпирические коэффициенты регрессии: b = 1.2948, a = 2.143
Уравнение регрессии (эмпирическое уравнение регрессии): y = 1.2948 x + 2.143

Пример №2.
1. Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с β₁ и β₂, пояснить различия между ними.
2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
3. Рассчитать общий и частные F-критерии Фишера.

Решение. Пояснения: задачу решаем с помощью сервиса Уравнение множественной регрессии для двух переменных

1. Расчет коэффициентов множественной линейной регрессии.
Система трех линейных уравнений с тремя неизвестными b₀, b₁, b₂:
∑y_i = nb₀ + b₁∑x_1i + b₂∑x_2i
∑x_1iy_i = b₀∑x_1i + b₁∑x_1i² + b₂∑x_1ix_2i
∑x_2iy_i = b₀∑x_2i + b₁∑x_1ix_2i + b₂∑x_2i²

Y	X₁	X₂	X₁²	X₂²	X₁Y	X₂Y	X₁X₂	Y²
4.07	182.94	1018	33467.04	1036324	744.57	4143.26	186232.92	16.56
4	193.45	920	37422.9	846400	773.8	3680	177974	16
2.98	160.09	686	25628.81	470596	477.07	2044.28	109821.74	8.88
2.2	157.99	405	24960.84	164025	347.58	891	63985.95	4.84
2.83	123.83	683	15333.87	466489	350.44	1932.89	84575.89	8.01
3	152.02	530	23110.08	280900	456.06	1590	80570.6	9
2.35	130.53	525	17038.08	275625	306.75	1233.75	68528.25	5.52
2.04	137.38	418	18873.26	174724	280.26	852.72	57424.84	4.16
1.97	137.58	425	18928.26	180625	271.03	837.25	58471.5	3.88
1.02	118.78	161	14108.69	25921	121.16	164.22	19123.58	1.04
1.44	142.9	242	20420.41	58564	205.78	348.48	34581.8	2.07
1.22	99.49	226	9898.26	51076	121.38	275.72	22484.74	1.49
1.11	116.17	162	13495.47	26244	128.95	179.82	18819.54	1.23
0.82	185.66	70	34469.64	4900	152.24	57.4	12996.2	0.67
31.05	2038.81	6471	307155.61	4062413	4737.04	18230.79	995591.55	83.37
2.22	145.63	462.21	21939.69	290172.36	338.36	1302.2	71113.68	5.95

Для наших данных система уравнений имеет вид:
31.05 = 14 b₀ + 2038.81b₁ + 6471b₂
4737.0435 = 2038.81b₀ + 307155.6083b₁ + 995591.55b₂
18230.79 = 6471b₀ + 995591.55b₁ + 4062413b₂
Решая систему методом Крамера, находим:
b₀ = 0.1804
b₁ = 0.003
b₂ = 0.0035
Уравнение регрессии: Y=0.1804+0.003X₁+0.0035X₂

Y	X₁	X₂	(Y_i-Y_ср)²	(X_1i-X_1ср)²	(X_2i-X_2ср)²	(Y_i-Y_ср)(X_1i-X_1ср)	(Y_i-Y_ср)(X_2i-X_2ср)	(X_1i-X_1ср)(X_2i-X_2ср)
4.07	182.94	1018	3.43	1392.09	308897.76	69.1	1029.39	20736.76
4	193.45	920	3.18	2286.82	209567.76	85.22	815.84	21891.64
2.98	160.09	686	0.58	209.11	50080.05	11.02	170.56	3236.1
2.2	157.99	405	0.0003	152.79	3273.47	-0.22	1.02	-707.21
2.83	123.83	683	0.37	475.21	48746.33	-13.34	135.15	-4812.97
3	152.02	530	0.61	40.84	4594.9	5	53.02	433.2
2.35	130.53	525	0.0175	227.99	3942.05	-2	8.3	-948.02
2.04	137.38	418	0.0316	68.05	1954.9	1.47	7.86	364.74
1.97	137.58	425	0.0614	64.79	1384.9	2	9.22	299.55
1.02	118.78	161	1.43	720.88	90730.05	32.16	360.81	8087.39
1.44	142.9	242	0.61	7.45	48494.33	2.12	171.3	601.03
1.22	99.49	226	1	2128.83	55797.19	46.04	235.71	10898.76
1.11	116.17	162	1.23	867.85	90128.62	32.64	332.59	8844.1
0.82	185.66	70	1.95	1602.46	153832.05	-55.96	548.26	-15700.62
31.05	2038.81	6471	14.5	10245.16	1071424.36	215.25	3879.04	53224.44
2.22	145.63	462.21	1.04	731.8	76530.31	15.38	277.07	3801.75

2. Анализ качества эмпирического уравнения множественной линейной регрессии.
Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям:
• проверка статистической значимости коэффициентов уравнения регрессии;
• проверка общего качества уравнения регрессии;
• проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).
Прежде чем проводить анализ качества уравнения регрессии, необходимо определить дисперсии и стандартные ошибки коэффициентов, а также интервальные оценки коэффициентов.
При этом:

где m=2 – количество объясняющих переменных модели.

Стандартные ошибки коэффициентов:

Y(X₁,X₂)	e_i = (Y_i-Y(X₁,X₂))	e_i²
4.26	-0.19	0.0357
3.95	0.0503	0.0025
3.04	-0.058	0.0034
2.06	0.14	0.0208
2.92	-0.09	0.0081
2.47	0.53	0.28
2.39	-0.0411	0.0017
2.04	0.0002	0
2.06	-0.0947	0.009
1.09	-0.0721	0.0052
1.44	-0.0049	0
1.26	-0.0406	0.0016
1.09	0.0222	0.0005
0.97	-0.15	0.0239
31.05	-0	0.39
2.22	0	0.0279

3. Оценка мультиколлинеарности факторов.
Парные коэффициенты корреляции.
Для y и x₁
Средние значения

Дисперсия

Среднеквадратическое отклонение

Коэффициент корреляции

Для y и x₂
Средние значения

Дисперсия

Среднеквадратическое отклонение

Коэффициент корреляции

Для x₁ и x₂
Средние значения

Дисперсия

Среднеквадратическое отклонение

Коэффициент корреляции

Матрица парных коэффициентов корреляции.

-	y	x₁	x₂
y	1	0.56	0.98
x₁	0.56	1	0.51
x₂	0.98	0.51	1

3. Оценка мультиколлинеарности факторов.
При оценке мультиколлинеарности факторов следует учитывать, что чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии.
Для отбора наиболее значимых факторов x_i учитываются следующие условия:
- связь между результативным признаком и факторным должна быть выше межфакторной связи;
- связь между факторами должна быть не более 0.7;
- при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними;
Более объективную характеристику тесноты связи дают частные коэффициенты корреляции, измеряющие влияние на результат фактора xi при неизменном уровне других факторов.
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и x_i) при условии, что влияние на них остальных факторов (x_j) устранено.

Теснота связи не сильная

Теснота связи сильная

Теснота связи не сильная

Теснота связи низкая.

Теснота связи сильная

Теснота связи низкая.
Уравнение регрессии в стандартизированном масштабе.
Другим видом уравнения множественной регрессии может быть уравнение регрессии в стандартизированном масштабе: t_y = β₁t_x1 + β₂t_x2.
где

β_i – стандартные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизированном масштабе применим МНК. Стандартизированные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:
r_yx1 = β₁ + β₂r_x2x1
r_yx2 = β₁r_x2x1 + β₂
Связь коэффициентов множественной регрессии b_i со стандартизированными коэффициентами β_i описывается соотношением:

Параметр α определяется как:
α=y-β₁·x₁-β₂·x₂

α=14.5-0·145.63-0·462.21=12.46
4. Оценка тесноты связи.
4. Теснота связи результативного признака с факторными определятся величиной коэффициента линейной множественной корреляции и детерминации, который могут быть исчислены на основе матрицы парных коэффициентов корреляции:

Более объективную оценку качества построенной модели дает скорректированный индекс множественной детерминации, учитывающий поправку на число степеней свободы:

где n- число наблюдений, m – число факторов.

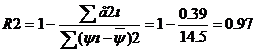
Сравнительная оценка влияния анализируемых факторов на результативный признак.
5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится:
- средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при измени фактора x_i на 1% от своего среднего значения;
- β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение S_xi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения;
- долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d²_i = r_yxiβ_i.
При этом должно выполняться равенство:
d²₁ + d²₂ = R²_yx1x2.
Результаты сравнительного анализа факторов оформляются в таблице:
6. Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента.
Оценка значимости коэффициентов регрессии b₁ и b₂ производится с помощью t-критерия Стьюдента и связана с сопоставлением их значений с величиной случайных ошибок mb1 и mb2. Более простым способом расчета фактических значений t_b1 и t_b2 является их определение через критерии F:
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит (n-m-1;α/2) = (11;0.025) = 2.201

Поскольку 0.638 < 2.201, то статистическая значимость коэффициента регрессии b₀ не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 1.3733 < 2.201, то статистическая значимость коэффициента регрессии b₁ не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 17.3651 > 2.201, то статистическая значимость коэффициента регрессии b₂ подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b_j - t_крит S_bj; b_j + t_крит S_bj)
(0.1804 - 2.201 • 0.2828; 0.1804 + 2.201 • 0.2828)
(-0.442;0.8028)
С вероятностью 95% можно утверждать, что значение данного параметра b₀ будут лежать в найденном интервале.
(0.003 - 2.201 • 0.0022; 0.003 + 2.201 • 0.0022)
(-0.0018;0.0077)
С вероятностью 95% можно утверждать, что значение данного параметра b₁ будут лежать в найденном интервале.
(0.0035 - 2.201 • 0.0002; 0.0035 + 2.201 • 0.0002)
(0.003;0.0039)
С вероятностью 95% можно утверждать, что значение данного параметра b₂ будут лежать в найденном интервале.
7. Проверка гипотезы о статистической значимости уравнения регрессии.
Проверка гипотезы H₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R² = 0) производится по F-критерию Фишера сравнением F_факт с F_табл.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

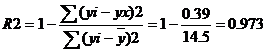
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=2 для множественной регрессии с двумя факторами.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 2 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2-1.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k₁=2 и k₂=11, Fkp = 3.98
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Частные критерии.
Частные критерии F_x1 и F_x2 оценивают статистическую значимость включения факторов x₁ и x₂ в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. F_x1 оценивает целесообразность включения в уравнение x₁ после включения в него фактора x₂.
Соответственно F_x2 указывает на целесообразность включения в модель фактора x2 после включения фактора x₁.

Поскольку фактическое значение F < Fkp, то коэффициент F_x1 статистически не значим, т.е. не целесообразно включать в уравнение x₁ после включения в него фактора x₂.

Поскольку фактическое значение F < Fkp, то коэффициент F_x2 статистически не значим, т.е. не целесообразно включать в уравнение x₂ после включения в него фактора x₁.
Проверка наличия предпосылок МНК.
1. первая предпосылка МНК – случайный характер остатков ε_i. Для проверки этого свойства определяют значения ε_i и строится график зависимости ε_i от теоретических значений результативного признака.
Если на графике получена горизонтальная полоса остатков ε_i то они представляют собой случайные величины и МНК оправдан, теоретические значения y_x независимы от ε_i.
При этом возможны следующие случаи, если ε_i зависит от y_x:
- остатки ε_i не случайны;
- остатки ε_i не имеют постоянной дисперсии;
- остатки ε_i носят систематический характер.
2. Вторая предпосылка МНК – нулевая средняя величина остатков, не зависящая от ε_i. Для проверки этой предпосылки строится график зависимости случайных остатков ε_i от факторов, включенных в регрессию x_i.
Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений x_i. Если же график показывает зависимости ε_i от x_i, то это свидетельствует о наличии систематической погрешности модели, причины которой могут быть разные.
Возможно, нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора x_i. Может быть, неправильно подобрана модель.
Корреляция случайны остатков с факторными признаками, позволяет проводить корректировку модели, например, использовать кусочно-линейные модели.
3. В соответствии с третей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора x_i остатки ε_i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.
Проверка на наличие гетероскедастичности.
a) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X_i, а по оси ординат квадраты отклонения ε_i².
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии гетероскедастичности.
b) При помощи теста ранговой корреляции Спирмена.
4. При построение регрессионных моделей важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения остатков ε_i распределены независимо друг от друга.
Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент автокорреляции определяется по формуле линейного коэффициента корреляции:

Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
Пятая предпосылка МНК о нормальном распределении остатков может быть визуально проверена путем графического изображения ряда распределения остаточных величин и сравнения с кривой нормального распределения.
О соответствии эмпирического распределения теоретическому можно судить по величине эксцесса (Е≈0).

где М4 – центральный момент четвертого порядка, который определяется по формуле :

Уравнение двухфакторной множественной регрессии

Правила ввода данных

Поиск

Процесс

Сообщение