Методические рекомендации к решению курсовой работы

1.Линейная производственная задача
Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов

компактно записаны в виде

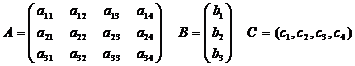
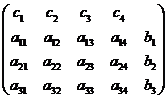
Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать узкие места производства.
В последней симплексной таблице указать обращенный базис Q^-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения H = Q^-1B.

Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.

2. Двойственная задача
Сформулировать задачу, двойственную линейной производственной задаче, как задачу определения расчетных оценок ресурсов, и найти ее решение, пользуясь второй основной теоремой двойственности (о дополняющей нежесткости). Указать оценку единицы каждого ресурса, минимальную суммарную оценку всех ресурсов, оценки технологий.

3. Задача «о расшивке узких мест производства»
Сформулировать задачу о "расшивке узких мест производства" и составить математическую модель. Определить область устойчивости двойственных оценок, где сохраняется структура программы производства. Решить задачу о ²расшивке узких мест производства² при условии, что дополнительно можно получить от поставщиков не более одной трети первоначально выделенного объема ресурса любого вида (если задача окажется с двумя переменными, то только графически); найти план приобретения дополнительных объемов ресурсов, дополнительную возможную прибыль.

5.Задача распределения капитальных вложений
Методом динамического программирования решить задачу распределения капитальных вложений между четырьмя предприятиями производственного объединения, располагающего суммой в 700 тыс. руб., по исходным данным, приведенным в приложении 3 (выделяемые суммы кратны 100 тыс.).

8. Задача о максимальном потоке в сети
Рассмотреть задачу о максимальном потоке в сети. Решить конкретную задачу на сети с 8-9 вершинами, предложив исходные данные самостоятельно.

16. Анализ доходности и риска финансовых операций
Провести анализ доходности и риска финансовых операций по исходным данным.
Даны четыре операции Q₁, Q₂, Q₃, Q₄. Найдите средние ожидаемые доходы Q_i и риски r_i операций. Нанесите точки (Q_i, r_i) на плоскость, найдите операции, оптимальные по Парето. С помощью взвешивающей формулы найдите среди таких операций лучшую.
Взвешивающая формула: φ(Q_i)=2Q_i-r_i.
Ряды распределений доходов операций Q₁, Q₂, Q₃, Q₄взять из приложения 1: по первой букве своей фамилии найти номер N, а затем надо взять из приложения 1 данные с номерами N, N+1, N+2, N+3. Например, если N=3, то берем данные с номерами 3, 4, 5, 6, т.е.
3. (0,1/4) (4,1/4) (6,1/3) (12,1/6) 4. (2,1/4) (6,1/4) (8,1/3) (14,1/6)
5. (0,1/3) (1,1/3) (2,1/6) (8,1/6) 6. (2,1/3) (3,1/4) (4,1/6) (10,1/6)
Следовательно, ряды распределений операций будут:

Q₁	:	0	4	6	12	Q₂:	2	6	8	14
		1/4	1/4	1/3	1/6		1/4	1/4	1/3	1/6

Q₃	:	0	1	2	8	Q₄	2	3	4	10
		1/3	1/3	1/6	1/6		1/3	1/3	1/6	1/6

Рекомендации к решению

1. Линейная производственная задача

Предположим, что предприятие или цех выпускает n видов изделий, имея m групп оборудования. Известны нормы времени на обработку каждого изделия на каждой группе оборудования, например, в минутах или часах и фонд времени работы каждой группы оборудования. Пусть, кроме того, известно, что из всех n видов изделий наибольшим спросом пользуются k видов. Требуется составить план производства, при котором выпуск дефицитных изделий будет наибольшим возможным.
Примем следующие обозначения:
i – номер группы оборудования (i=1,2, … , m);
j – номер вида изделия (j=1,2, … , n);
a_ij – норма времени на обработку единицы i-го изделия на j-ой группе оборудования;
b_i – действительный фонд времени работы i-й группы оборудования;
x_i – планируемое количество единиц j-го изделия;
(x₁, x₂, … , x_n) – искомый план производства.
Какова бы ни была производственная программа (x₁, x₂, … , x_n), ее компоненты должны удовлетворять условию, что суммарное время обработки всех изделий на данной группе оборудования не должно превышать фонда времени работы этой группы оборудования. На обработку x₁ единиц первого изделия на i-й группе оборудования будет затрачено a_i1x₁единиц времени, на обработку x₂ единиц второго изделия на той же группе оборудования будет затрачено a_i2x₂ единиц времени и т.д. Необходимое время на обработку всех x₁, x₂, … , x_nизделий на i-й группе оборудования будет равно сумме

a_i1x₁ + a_i2x₂ + .. + a_nx_n
Эта сумма не может превышать фонд времени работы i-й группы оборудования, т.е. должна быть £ b_i. Выписывая такие условия для всех m групп оборудования, получаем:
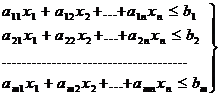(1)
Так как компоненты плана суть количество изделий и, следовательно, не могут быть выражены отрицательными числами, то добавляются условия:

x₁ ≥0, x₂,≥0,…,x_n≥0 (2)
Обозначим через с_jприбыль на единицу j-го изделия. При плане производства (х₁, х₂, …, х_n) прибыль предприятия будет равна:
z = c₁x₁ + c₂x₂ + … + c_nx_n. (3)
Мы хотим составить производственную программу (х₁, х₂, …, х_n) так, чтобы функция (3) приняла наибольшее значение при выполнении всех других условий.
Система линейных неравенств (1), (2) и линейная форма (3) образуют математическую модель задачи о рациональном использовании производственных мощностей. Среди всех решений системы линейных неравенств (1), удовлетворяющих условию неотрицательности (2), необходимо найти такое решение, при котором линейная форма (3) принимает наибольшее возможное значение. Это – задача линейного программирования.
Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли:
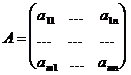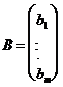, , C=(c₁, …, c_n)
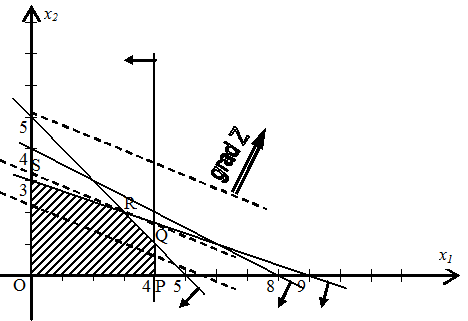
В качестве примера рассмотрим задачу оптимизации производственной программы цеха, который может выпускать два вида изделий, имея четыре группы производственного оборудования. Пусть
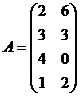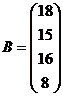, , C=(6 9), или кратко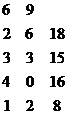
Задача состоит в том, чтобы найти производственную программу, максимизирующую прибыль:

z = 6x1 + 9x2 (4)
при условиях:
2x₁+x₂≤18 (5)
3x₁+x₂≤15
4x₁≤16
x₁+2x₂≤8
x₁ ≥ 0, x₂ ≥ 0 (6)
Полученную задачу линейного программирования с двумя переменными можно решить графически. Система линейных неравенств (5), (6) определяет выпуклый многоугольник OPQRS допустимых решений. Линии уровня функции Z перпендикулярны вектору-градиенту grad Z=(6,9) и образуют семейство параллельных прямых (градиент указывает направление возрастания функции). Наибольшего значения функция Z достигает в точке R. Координаты этой точки определяют оптимальный план производства x₁=3, x₂=2, а максимальная прибыль будет равна 36.

Последовательное улучшение производственной программы.
Предположим теперь, что предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли

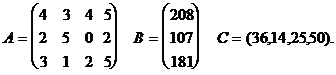(7)

Требуется составить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах

Математическая модель задачи:
найти производственную программу
(x₁, x₂, x₃, x₄)
максимизирующую прибыль
z = 36x₁+ 14x₂ + 25x₃ + 50x₄ (8)
при ограничениях по ресурсам
4x₁+3x₂+4x₃+5x₄≤208 (9)
2x₁+5x₂+2x₄≤107
3x₁+x₂+2x₃+5x₄≤181
где по смыслу задачи x₁≥0, x₂≥0, x₃≥0, x₄≥0. (10)
Получили задачу на условный экстремум. Для ее решения систему неравенств (9) при помощи дополнительных неотрицательных неизвестных х₅, х₆, х₇ заменим системой линейных алгебраических уравнений
4x₁+3x₂+4x₃+5x₄+x₅=208 (11)
2x₁+5x₂+2x₄+x₆=107
3x₁+x₂+2x₃+5x₄+x₇=181
где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (11), удовлетворяющих условию неотрицательности:

x_i≥0, i=1,...,7 (12)
надо найти то решение, при котором функция (8) примет наибольшее значение.

Эту задачу решим симплекс-методом.
Процесс решения обычно записывается в виде некоторой таблицы, представляющей собой последовательность симплексных таблиц, соответствующих итерациям симплекс-метода.

В последней симплексной таблице получено оптимальное решение задачи (8),(11),(12): x₁=27, x₂=0, x₃=0, x₄=20, x₅=0, x₆=13, x₇=0
Компоненты этого решения определяют производственную программу
x₁=27, x₂=0, x₃=0, x₄=20
остатки ресурсов:
первого вида х₅=0
второго вида х₆=13
третьего вида х₇=0
Следует обратить внимание на экономический смысл элементов последней строки последней симплексной таблицы. Например, коэффициент D₃=7 при переменной х₃ показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц.
В заключение заметим, что в рассматриваемом простейшем примере линейной производственной задачи возможна самопроверка результата.
Воспользуемся тем, что в оптимальной производственной программе х₂=0, х₃=0. Предположим, что вторую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:
z=36x₁+50x₄ → max
4x₁+5x₄≤208
2x₁+2x₄≤107
3x₁+5x₄≤181
x₁≥0, x₄≥0
x(x₁, x₄) - ?
Это задача линейного программирования с двумя переменными. Ее следует решить графически и убедиться, что результаты совпадают.

2. Двойственная задача

Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям. Пусть в условиях этой задачи требуется дать оценку каждому ресурсу. Оценка ресурса должна показывать, насколько увеличится прибыль, если количество ресурса увеличить на единицу.
Чтобы решить эту задачу представим себе, что возникла новая ситуация. Знакомый предприниматель П., занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у₁ рублей за каждую единицу первого ресурса, у₂ руб. – второго, у₃ руб. – третьего. Возникает вопрос: при каких ценах у₁, у₂, у₃ мы можем согласиться с этим предложением, чтобы выручка от продажи ресурсов скомпенсировала потерю прибыли, вызванную продажей ресурсов.
Величины у₁, у₂, у₃ принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид

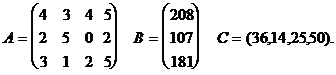
Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 4 единицы ресурса первого вида, 2 единицы ресурса второго вида и 3 единицы третьего (элементы первого столбца матрицы). В ценах у₁, у₂, у₃ наши затраты составят 4у₁+ 2у₂+ 3у₃, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы первой продукции. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше

4у₁+ 2у₂+ 3у₃³ 36.

Аналогично, во втором столбце матрицы А указаны затраты различных ресурсов на производство единицы продукции второго вида. В ценах П эти затраты составят 3у₁+ 5у₂+ у₃, а на рынке за единицу продукции второго вида мы получили бы прибыль 14 рублей. Поэтому перед предпринимателем П мы ставим условие

3у₁+ 5у₂+ у₃³ 14

и т.д. по всем видам продукции.

Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 208у₁+ 107у₂+ 181у₃ рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у₁, у₂, у₃, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.

Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок

у(у₁, y₂, y₃)
минимизирующий общую оценку всех ресурсов
f = 208y₁ + 107y₂ +181y₃(1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
4y₁+ 2y₂+ 3y₃ ≥ 36
3y₁+ 5y₂+ y₃≥ 14
4y₁+ 2y₃≥ 25
5y₁+ 2y₂+ 5y₃≥ 50
причем оценки ресурсов не могут быть отрицательными
y₁≥0, y₂≥0, y₃≥0. (3)
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальности допустимых решений (х₁, х₂, х₃, х₄) и (y₁, y₂, y₃) пары двойственных задач необходимо и достаточно выполнение условий

x ₁ (4y₁+ 2y₂+ 3y₃ - 36) = 0

x ₂ (3y₁+ 5y₂+ y₃- 14) = 0

x ₃(4y₁+ 2y₃- 25) = 0

x ₄(5y₁+ 2y₂+ 5y₃- 50) = 0

y₁ (4x₁ +3x₂+ 4x₃+ 5x₄- 208) = 0

y₂ (2x₁ +5x₂+ 2x₄- 107) = 0

y₃ (3x₁ + x₂+ 2x₃+ 5x₄- 181) = 0

Ранее было найдено, что в решении исходной задачи х₁>0, x₄>0. Поэтому
4y₁+ 2y₂+ 3y₃ - 36 = 0
5y₁+ 2y₂+ 5y₃- 50 = 0
Если же учесть, что второй ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю
у₂=0,
то приходим к системе уравнений:
4y₁+ 3y₃ - 36 = 0
5y₁+ 5y₃- 50 = 0
откуда следует
у₁=6, у₃=4.
Таким образом, получили двойственные оценки ресурсов
у₁=6; у₂=0; у₃=4, (4)
причем общая оценка всех ресурсов равна 1972.
Заметим, что решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка третьего ресурса у₃=4 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 4 единицы.

3. Задача о "расшивке узких мест производства"

Пусть в условиях линейной производственной задачи планируется расширить производство за счет приобретения дополнительных объемов тех ресурсов, которые по оптимальному плану израсходованы полностью. Требуется составить план приобретения дефицитных ресурсов, который обеспечит максимальный прирост прибыли при условии сохранения структуры производства, т.е. набора видов продукции, которые производятся по оптимальному плану. Решить задачу при дополнительном условии: объем дополнительно приобретаемых ресурсов не должен превышать одной трети первоначального объема ресурсов.
Составим математическую модель задачи. При выполнении оптимальной производственной программы первый и третий ресурсы используются полностью, т.е. образуют ²узкие места производства². Будем их заказывать дополнительно.
Пусть T(t₁,t₂,t₃)- вектор дополнительных объемов ресурсов. Условие сохранения структуры производства математически выражается так:

H + Q^-1T ≥ 0.
Заметим, что это условие определяет также область устойчивости двойственных оценок ресурсов, поэтому можно использовать двойственные оценки ресурсов, найденные при решении двойственной задачи. Задача состоит в том, чтобы найти вектор T (t₁, 0, t₃), максимизирующий суммарный прирост прибыли
W = 6t₁ + 4t₃ (1)
при условии сохранения двойственных оценок ресурсов (и структуры производственной программы)

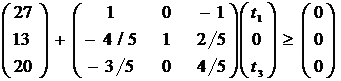
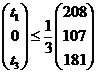предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида

, (3)
причем по смыслу задачи
t₁ ≥ 0, t₃ ≥ 0. (4)
Переписав неравенства (2) и (3) в виде:
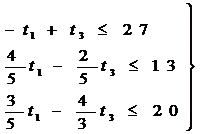(5)
t₁≤208/3; t₃ ≤ 181/3 (6)
приходим к задаче ЛП:

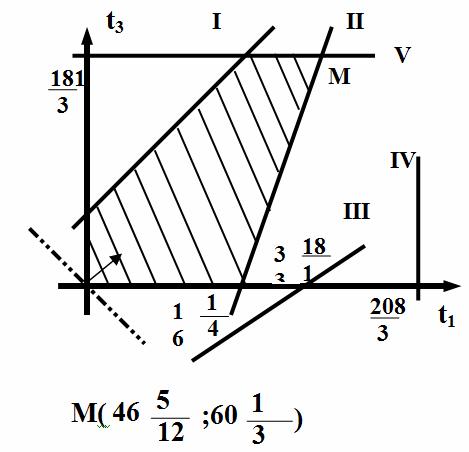
максимизировать (1) при условиях (5), (6) и (4). Эту задачу легко решить графически (см. рис.).
Программа расшивки имеет вид: t₁ = 46 ⁵/₁₂; t₃ = 60 ¹/₃ и прирост прибыли составит 519 ²/₃.
Отметим, что все вышеизложенное можно получить с помощью решения двойственной задачи линейного программирования.

4. Задача распределения капитальных вложений

Динамическое программирование - это вычислительный метод для решения задач управления определенной структуры. Данная задача с n переменными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.
Знакомство с методом динамического программирования проще всего начать с рассмотрения нелинейной задачи распределения ресурсов между предприятиями одного производственного объединения или отрасли. Для определенности можно считать, что речь идет о распределении капитальных вложений.
Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через f_i(x_i) прирост мощности или прибыли на j-м предприятии, если оно получит x_i рублей капитальных вложений. Требуется найти такое распределение (x₁,x₂, ... , x_n) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли
z = f₁(x₁) + f₂(х₂) + ... + f_n(x_n)
при ограничении по общей сумме капитальных вложений

x₁ + x₂ + ... + x_n = b .
причем будем считать, что все переменные x_j принимают только целые неотрицательные значения. Функции f_j(x_j) мы считаем заданными, заметив, что их определение - довольно трудоемкая экономическая задача.
Воспользуемся методом динамического программирования для решения этой задачи.
Введем параметр состояния и определим функцию состояния. За параметр состояния x примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния F_k(x) определим как максимальную прибыль на первых k предприятиях, если они вместе получают x рублей. Параметр x может изменяться от 0 до b. Если из x рублей k-е предприятие получит x_k рублей, то каково бы ни было это значение, остальные x - x_k рублей естественно распределить между предприятиями от первого до (К-1)-го так, чтобы была получена максимальная прибыль F_k-1(x - x_k). Тогда прибыль k предприятий будет равна f_k(x_k) + F_k-1(x - x_k). Надо выбрать такое значение x_k между 0 и x, чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению:
F_k(x)=max{f_k(x_k) + F_k-1(x-x_k)}
0 £ x_k£ x
для k = 2, 3, 4, ... , n . Если же k=1, то
F₁(x) = f₁(x)
Рассмотрим конкретный пример. Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций f_j(x_j) приведены в таблице 1, где, например, число 88 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 88 тыс. руб.

Таблица I

x_i	100	200	300	400	500	600	700
f₁(x₁)	20	34	46	53	55	60	60
f₂(x₂)	18	29	45	62	78	90	98
f₃(x₃)	25	41	52	74	82	88	90
f₄(x₄)	30	52	76	90	104	116	125

Прежде всего, заполняем табл. 2. Значения f₂(x₂) складываем со значениями F₁(x - x₂) = f₁(x- x₂) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение

. Заполняем таблицу 3.
Продолжая процесс, табулируем функции F₃(x),

(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
Z_max = 155 тыс. руб.,
причем четвертому предприятию должно быть выделено
х^*₄=

4(700) = 300 тыс. руб.
На долю остальных трех предприятий остается 400 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено
x^*₃ =

3 (700-x^*₄) =

3(400) = 200 тыс. руб.
Продолжая обратный процесс, находим
x*₂ =

2 (700 - x*₄ - x*₃) =

2 (200) = 100 тыс. руб.
На долю первого предприятия остается
x*₁ = 700 - x*₄ - x*₃ - x*₂ = 100 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*₁ =100; x*₂ =100; x*₃ = 200; x*₄ = 300.
Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 155 тыс. руб.
Студенту рекомендуется проверить выполнение равенства
f₁(x*₁) + f₂(x*₂) + f₃(x*₃) + f₄(x*₄) = z _max

Таблица 2

	x - x₂	0 100 200 300 400 500 600 700
x2	F₁(x - x₂) f₂(x₂)	0 20 34 46 53 55 60 60
0	0	0 20* 34 46 53 55 60 60
100	18	18 38* 52* 64 71 73 78
200	29	29 49 63 75 82 84
300	45	45 65* 79 91 98
400	62	62 82* 96 108
500	78	78 98* 112*
600	90	90 110
700	98	98 .

Таблица 3

x	0 100 200 300 400 500 600 700
F₂(x)	0 20 38 52 65 82 98 112
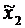(x)	0 0 100 100 300 400 500 500

Таблица 4

	x - x₃	0 100 200 300 400 500 600 700
x3	F₂(x - x₃) f₃(x₃)	0 20 38 52 65 82 98 112
0	0	0 20 38 52 65 82 98 112
100	25	25* 45* 63* 77 90 107 123
200	41	41 61 79* 93 106 123
300	52	52 72 94* 112 126
400	74	74 94* 112* 126*
500	82	82 102 120
600	88	88 106
700	90	90 .

Таблица 5

x	0 100 200 300 400 500 600 700
F₃(x)	0 25 45 63 79 94 112 126
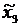(x)	0 100 100 100 200 400 400 400

Таблица 6

	x - x₄	0 100 200 300 400 500 600 700
x4	F₃(x - x₄) f₄(x₄)	0 25 45 63 79 94 112 126
0	0	126
100	30	142
200	52	146
300	76	155*
400	90	153
500	104	149
600	116	141
700	125	125 .

5. Анализ доходности и риска финансовых операций

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку, и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками.
Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль, так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию).
Как оценить операцию с точки зрения ее доходности и риска?
Существует несколько разных способов. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.
Рассмотрим какую-нибудь операцию, доход которой есть случайная величина Q. Средний ожидаемый доход (доходность) Q - это математическое ожидание с.в. Q: Q=∑q_i·p_i, где p_i есть вероятность получить доход q_i. А среднее квадратическое отклонение (СКО)

- это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать s количественной мерой риска операции и обозначить r. Напомним, что дисперсия
D[Q] = M [(Q - Q)²] = M [Q²] - Q².
Рассмотрим четыре операции Q₁, Q₂, Q₃, Q_,4. Найдем средние ожидаемые доходы Q_i и риски r_i операций.
Ряды распределения, средние ожидаемые доходы и риски:

Q₁	:	5	2	8	4	Q₁= 29/6 ≈ 4.81	r₁ ≈ 1.77
		1/2	1/6	1/6	1/6

Q₂	:	2	3	4	12	Q₂= 25/6 = 4.16	r₂ ≈ 3.57
		1/2	1/6	1/6	1/6
Q₃	:	8	5	3	10	Q₃= 7	r₃ = 2.30
		1/2	1/6	1/6	1/6

Q₄	:	1	4	2	8	Q₄= 17/6 ≈ 2.81	r₄ = 2.54
		1/2	1/6	1/6	1/6

Напомним, как находить Q и r.
Q₁=∑q_i·p_i= 5*1/2+2*1/6+8*1/6+4*1/6=29/6

;
MQ₁² = 25*1/2+4*1/6+64*1/6+16*1/6=159/6;
Q1² = 841/36; D [Q₁] = (159*6-841)/36 = 113/36;

Нанесем средние ожидаемые доходы Q и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):

Можно также использовать калькулятор Показатели вариации.

Получили 4 точки. Чем правее точка (Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (Q*, r*) доминирует точку (Q, r), если Q* <Q и r* < r. В нашем случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы - доходность 3-й больше, но и риск ее тоже больше.
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето. В рассматриваемом примере операции Q₁ и Q₃ оптимальны по Парето.
Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть φ(Q_i)=2Q_i-r_i. Тогда получаем:
φ(Q₁)= 2·4.81-1.77 = 7.85; φ(Q₃)= 11.70;
Таким образом, 3-я операция - лучшая.

Решить аналогичную задачу онлайн

6. Формирование оптимального портфеля ценных бумаг

На финансовом рынке обращается, как правило, множество ценных бумаг: государственные ценные бумаги, акции частных фирм, векселя и т.п. Ценная бумага удостоверяет возможность получения некоторого дохода. В общем случае владелец получит некоторый случайный доход.
Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Эффективность E есть некоторый обобщенный показатель дохода или прибыли. Будем считать E случайной величиной, ее математическое ожидание есть m_Е. При исследовании финансового рынка дисперсию обычно называют вариацией V, и рискованность обычно отождествляется со средним квадратическим отклонением. Таким образом, V=D[E]= M[(E- m_Е)²] и s =

.
Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг, по различным видам ценных бумаг. Пусть x_i - доля капитала, потраченная на закупку ценных бумаг i-го вида. Пусть E_i - эффективность (можно считать, доход за некоторый период времени) ценных бумаг i-го вида, стоящих одну денежную единицу. Через V_ij будем обозначать ковариацию ценных бумаг i-го и j -го видов (или корреляционный момент K_ij). Пусть m_i - математическое ожидание эффективности E_i и s_i=

, где V_ii - вариация или дисперсия этой эффективности E_i . Рискованность ценной бумаги i-го вида отождествим со средним квадратическим отклонением s_i.
Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Эффективность портфеля (в простейшем случае это доход, приносимый ценными бумагами портфеля за какой-нибудь промежуток времени), вообще говоря, есть случайная величина, обозначим ее через E_p, тогда ожидаемое значение этой эффективности m_p =M[E_p]=∑x_im_i. Дисперсия портфеля есть D[E_p]= ∑x_ix_jV_ij. Величина

может быть названа риском портфеля. Обычно D[E_p] обозначается V_p. Итак, мы выразили эффективность и риск портфеля через эффективности составляющих его ценных бумаг и их ковариации.
Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность побольше, а риск поменьше. Однако поскольку "нельзя поймать двух зайцев сразу", необходимо сделать определенный выбор между эффективностью и риском.
Математическая формализация задачи формирования оптимального портфеля такова:
найти значения x_i, минимизирующие вариацию эффективности портфеля
V_p = ∑x_ix_jV_ij,
при условии, что обеспечивается заданное значение ожидаемой
эффективности портфеля m_p, т.е.
m_p=∑x_im_j.
поскольку x_i - доли, то в сумме они должны составлять единицу:
∑x_i=1 .
Оптимальное решение этой задачи обозначим символом *. Если x^*_i >0 , то это означает рекомендацию вложить долю x^*_i наличного капитала в ценные бумаги i-го вида. Если же x^*_i < 0 , то содержательно это означает провести операцию "short sale". Если такие операции невозможны, значит необходимо ввести ограничения x_i³ 0 . Что такое операция "short sale"?
Если x^*_i< 0 , то инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги i-го вида (вместе с доходом, какой они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает более доходные ценные бумаги и получает по ним доход и оказывается в выигрыше!
Если на рынке есть безрисковые бумаги (к таким можно с некоторой натяжкой отнести государственные ценные бумаги), то решение задачи об оптимальном портфеле сильно упрощается и приобретает замечательное новое качество.
Пусть m₀ - эффективность безрисковых бумаг, а x₀ - доля капитала в них вложенного. Пусть m_r - средняя ожидаемая эффективность и V_r, s_r- вариация (дисперсия), СКО эффективности рисковой части портфеля, в рисковую часть портфеля вложено (1-x₀) часть всего капитала. Тогда ожидаемая эффективность всего портфеля m_p =x₀ m₀ +(1-x₀)m_r, вариация портфеля V_p =(1-x₀)² V_r и риск портфеля s_p =(1-x₀) s_r(считается, что безрисковые бумаги некоррелированы с остальными). Исключая x₀, получим
m_p = m₀ +s_p (m -m₀)/ s_r ,
т.е. ожидаемая эффективность портфеля линейно зависит от его риска.
Рассмотрим задачу об оптимальном портфеле в этом случае. Рисковые виды ценных бумаг будем нумеровать числами от 1 до n .

∑x_ix_jV_ij → min
x₀m₀ + ∑x_im_i = m_p

x₀ + ∑x_i = 1

Изложим теперь окончательное решение этой задачи.
Пусть V - матрица ковариаций рисковых видов ценных бумаг, X=(x_i), M=(m_i) - векторы-столбцы долей x_i капитала, вкладываемых в i-й вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, i=1,.., n. Пусть также I - n-мерный вектор-столбец, компоненты которого есть 1. Тогда оптимальное значение долей x_i есть

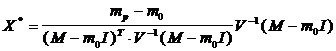
Здесь V^-1 - матрица, обратная к V . В числителе дроби стоит число, в знаменателе, если выполнить все действия (верхний индекс ^Т означает транспонирование вектора-столбца), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора, V^-1(M-m₀I) - вектор-столбец размерности n. Видно, что этот вектор не зависит от эффективности портфеля m_p. Таким образом, вектор долей рисковых видов ценных бумаг пропорциональный этому вектору также не зависит от m_p. Следовательно, структура рисковой части портфеля не зависит от m_p. Однако сумма компонент вектора X^* зависит от m_p, именно, компоненты вектора X^* пропорционально увеличиваются с ростом m_p, поэтому доля x₀ безрисковых вложений будет при этом сокращаться.
Пример. Сформировать оптимальный портфель заданной эффективности из трех видов ценных бумаг: безрисковых эффективности 2 и некоррелированных рисковых ожидаемой эффективности 4 и 10 и рисками 2 и 4 . Как устроена рисковая часть оптимального портфеля? При какой ожидаемой эффективности портфеля возникает необходимость в операции "short sale" и с какими ценными бумагами?
Решение. Итак, m₀=2, M=

, V=

. Зададимся эффективностью портфеля m_p. Теперь надо найти обратную матрицу к матрице V . Это просто: V^-1 =

. Вычислим знаменатель:

Итак, вектор долей рисковых бумаг есть X^* =((m_з-2)/5)

. Таким образом, рисковые доли должны быть одинаковы и каждая из них равна (m_з-2)/10. Следовательно, x^*₀ =1-(m_р-2)/5 . Необходимость в операции "short sale" возникнет, если x^*₀ < 0, т.е. когда m_р> 7 .
Можно доказать, что риск оптимального портфеля в зависимости от его доходности при наличии безрисковых бумаг равен (m_p-m₀)/d, где

Рассмотренную постановку задачи формирования оптимального портфеля можно словами сформулировать так: сформировать портфель, имеющий минимальный риск среди всех портфелей, имеющих эффективность не менее заданной. Но столь же естественна и задача формирования портфеля, имеющего максимальную эффективность среди всех портфелей, имеющих риск не более заданного, т.е. найти x_i, максимизирующие ожидаемую эффективность портфеля
mp = ∑x_i·m_i → max

при условии, что обеспечивается значение риска портфеля не более заданного,

т.е. ∑x_i·x_j·V_ij ≤V_p,

поскольку x_i – доли, то в сумме они должны составлять единицу: ∑x_i = 1
Если на рынке есть безрисковые бумаги, то в такой постановке задача формирования такого оптимального портфеля имеет решение, очень похожее на (2): Оптимальное значение долей x* рисковых бумаг есть

(3)

Можно доказать, что эффективность портфеля максимальной эффективности в зависимости от заданного его риска r_p равна m₀ + d∙r_p.

7. Задача принятия решений в условиях неопределенности

Предположим, что ЛПР (лицо, принимающее решения) рассматривает несколько возможных решений: i=1..m. Ситуация, в которой действует ЛПР, является неопределенной. Известно лишь, что наличествует какой-то из вариантов: j=1..n. Если будет принято i-e решение, а ситуация есть j-я , то фирма, возглавляемая ЛПР, получит доход q_ij. Матрица Q=(q_ij) называется матрицей последствий (возможных решений). Какое же решение нужно принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме?
Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть j-я , то было бы принято решение, дающее доход q_j = max(q_ij).
Значит, принимая _i-e решение мы рискуем получить не _qj, а только _qij, значит принятие _i-го решения несет риск недобрать r_ij=q_i-q_ij. Матрица R=(r_ij) называется матрицей рисков.

Пример 1. Пусть матрица последствий есть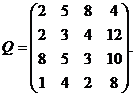
Составим матрицу рисков (см. как составить онлайн). Имеем q₁=max q_i1=8, q₂=5, q₃=8, q₄=12. Следовательно, матрица рисков есть

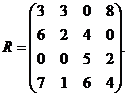
А. Принятие решений в условиях полной неопределенности

Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.
Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации?
Правило Вальда (правило крайнего пессимизма). Рассматривая _i-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход

.Но теперь уж выберем решение _i0 с наибольшим _ai0. Итак, правило Вальда рекомендует принять решение _i0, такое что

Так, в вышеуказанном примере, имеем a₁= 2, a₂ = 2, a₃ = 3, a₄ = 1_.Из этих чисел максимальным является число 3 . Значит, правило Вальда рекомендует принять 3-е решение.
Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков _R=(rij). Рассматривая _i-e решение будем полагать, что на самом деле складывается ситуация максимального риска

Но теперь уж выберем решение _i0 с наименьшим _bi0. Итак, правило Сэвиджа рекомендует принять решение _i0, такое что

В рассматриваемом примере имеем b₁ = 8, b₂=6, b₃=5, b₄=7_. Минимальным из этих чисел является число 5. Т.е. правило Сэвиджа рекомендует принять 3-е решение.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение i, на котором достигается максимум

, где 0≤λ≤1.
Значение λ выбирается из субъективных соображений. Если λ приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении λ к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при λ=½ правило Гурвица рекомендует 2-е решение.

В. Принятие решений в условиях частичной неопределенности

Предположим, что в рассматриваемой схеме известны вероятности p_j того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.
Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения, является случайной величиной Q_i с рядом распределения

q_i1	q_i2	…	q_in
p₁	p₂	…	p_n

Математическое ожидание M[Q] и есть средний ожидаемый доход, обозначаемый Q_i. Правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход. Предположим, что в схеме из предыдущего примера вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда Q₁=29/6, Q₂=25/6, Q₃=7, Q₄=17/6. Максимальный средний ожидаемый доход равен 7, соответствует третьему решению.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения, является случайной величиной R_j с рядом распределения

r_i1	r_i2	…	r_in
p₁	p₂	…	p_n

Математическое ожидание M[R_i] и есть средний ожидаемый риск, обозначаемый также R_i. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем R₁=20/6, R₂=4, R₃=7/6, R₄=32/5. Минимальный средний ожидаемый риск равен 7/6, соответствует третьему решению.
Анализ принимаемых решений по двум критериям: среднему ожидаемому доходу и среднему ожидаемому риску и нахождение решений, оптимальных по Парето, аналогично анализу доходности и риска финансовых операций. В примере множество решений, оптимальных по Парето операций, состоит только из одного 3-его решения.
В случае, если количество Парето-оптимальных решений больше одного, то для определения лучшего решения применяется взвешивающая формула f(Q)=2Q-R.

С. Правило Лапласа

Иногда в условиях полной неопределенности применяют правило Лапласа, согласно которому все вероятности p_j считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.