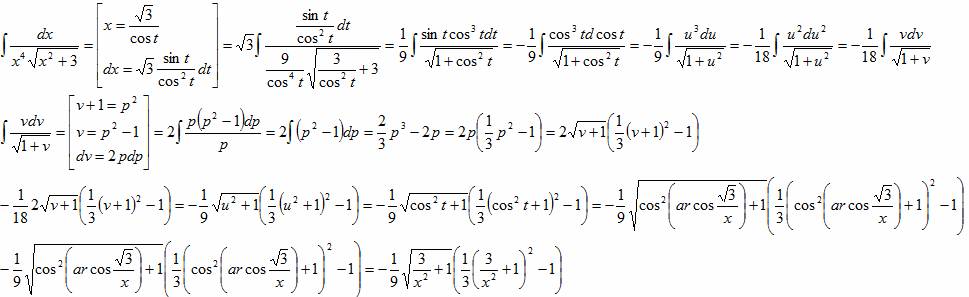Интегрирование простейших иррациональностей
Данный онлайн калькулятор служит для вычисления интегралов иррациональных дробей вида
, 
, 
.
Также рекомендуется ознакомиться с сервисом интегралы онлайн.
Пусть 
– рациональная функция от 
Эта функция, а следовательно, и интеграл от неё, рационализируется подстановкой x=tr, где r– наименьшее общее кратное чисел r1, r2,…, rn. Тогда dx=rtr-1 и под интегралом стоит рациональная функция от t. Аналогично, если подынтегральное выражение 
есть рациональная функция от 
, то подынтегральная функция рационализируется подстановкой 
где t – наименьшее общее кратное чисел r1, r2,…, rn. Тогда 
Подставляя в исходное выражение, получаем рациональную функцию от t.
Пример. Вычислить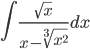 
. Наименьшее общее кратное чисел 2 и 3 равно 6. Поэтому делаем замену x = t6. Тогда dx = 6t5dt и
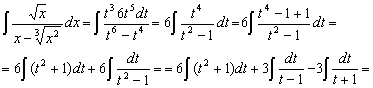
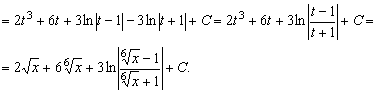
Интегрирование иррациональных функций
Пример №1. Вычислить определенный интеграл от иррациональной функции: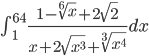
Решение. Интеграл вида R(xα1, xα2,..., xαk)dx, где R — рациональная функция от xαi, αi=pi/qi — рациональные дроби (i = 1,2,..., k), сводится к интегралу от рациональной функции с помощью подстановки х = tq, где q — наименьшее общее кратное (НОК) знаменателей дробей а1, а2,..., аk. В нашем случае а1 = 2, a2 = 3, a3 = 6, так что наименьшее общее кратное их знаменателей q = НОК(2,3,6) = 6. Замена переменной х = t6 приводит к интегралу от дробно-рациональной функции, который вычисляется, как описано в примере:
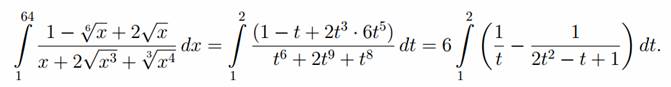
Ответ:
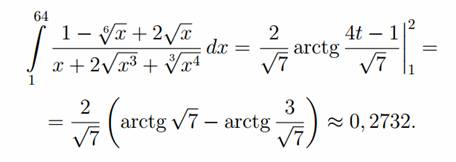
Пример №2.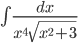 
Решение.
