Интегральное исчисление
Основные понятия и формулыНеопределенный интеграл
Определение 1: Функция F(x) называется первообразной для функции f(x), если выполняется равенствоF′(x)=f(x) или dF(x)=f(x)dx.
Определение 2: Совокупность всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
Основные свойства неопределенного интеграла
- (∫f(x)dx)′ = f(x)dx), d(∫f(x)dx) = f(x)dx;
- ∫d(f(x)) = f(x) + C
- ∫(f(x) ± g(x))dx = ∫f(x)dx ± ∫g(x)dx;
- ∫k·f(x)dx = k·∫f(x)dx;
Таблица интегралов
1.
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
| 10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
|
Методы вычисления
- Подведение под знак дифференциала.
- Интегрирование по частям.
- Простейшие преобразования подынтегрального выражения.
- Интегрирование рациональных дробей.
- Интегрирование иррациональных функций.
- Интегрирование выражений, содержащих тригонометрические функции.
Вычисление неопределенного интеграла методом подстановки (замены переменной)
Этот метод заключается в том, что заменяют переменную х на φ(t), где φ(t) - непрерывно дифференцируемая функция, полагают dx=φ′(t)dt и получают ∫f(x)dx|x=φ(t) = ∫f[φ(t)]φ′(t)dt. При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением t=ψ(x), которое находится из соотношения x=φ(t).
Определенный интеграл и его свойства
Определение 3: Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю: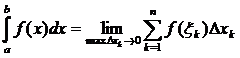
Свойства определенного интеграла
1.
2.
3.
4.
5.
, 
Формула Ньютона-Лейбница 
=F(b)-F(a)
Геометрический смысл определенного интеграла
Если функция на отрезке [a;b], то определенный интеграл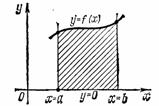
геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями y = f(x), x = a, x = b, y = 0( рис.5)
Рис. 5
Площадь криволинейной трапеции, ограниченной кривой y=f(x), [f(x)≥0], прямыми x=a, x=b и отрезком [a,b] оси ОХ, вычисляется по формуле
.
Площадь фигуры, ограниченной кривыми y=f1(x), y=f2(x), f1(x)≤f2(x), прямыми x=a, x=b, вычисляется по формуле
.
Пример 20: Вычислить неопределенный интеграл 
.
Решение:
=
5·sin(x)+2x-x3+ln|x|-4·arctg(x) + C.
Пример 21: Вычислить неопределенный интеграл 
.
Решение:=
.
Пример 22: Вычислить неопределенный интеграл 
Решение:=
Пример 23: Вычислить неопределенный интеграл 
Решение:
=
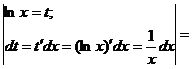
Пример 24: Вычислить неопределенный интеграл ∫ctg(x)dx
Решение:
Пример 25: Вычислить неопределенный интеграл 
Решение:
=
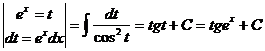
Пример 26: Вычислить определенный интеграл 
.
Решение:
=ln x|21 = ln(2)-ln(1)=ln(2)
Пример 27. Вычислить определенный интеграл: 
.
Решение:
.
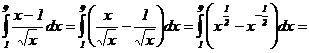
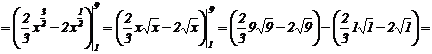
Пример 28. Вычислить определенный интеграл методом замены переменной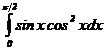 
Решение:
=
=
.
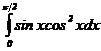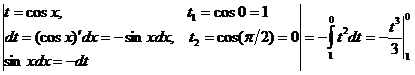Пример 29. Вычислить определенный интеграл: 
.
Решение:
.
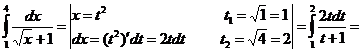
Пример 30. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями y=-x2+1, y=x-1.
Решение:
1. Сделаем чертеж.
Графиком функции y = -x2+1 является парабола, ветви которой направлены вниз. Найдем координаты вершины параболы: 
; 
; y0=y(x0)=0+1=1. Вершина параболы имеет координаты (0;1). Найдем точки пересечения параболы с осью ОХ: -x2+1=0, x2=1; x=±1. Точки пересечения с осью ОХ (-1;0) и (1;0).
| х | 0 | 1 |
| у | -1 | 0 |
Графиком функции
y=x-1 является прямая. Для построения прямой достаточно двух точек
Сделаем чертеж (рис.6).
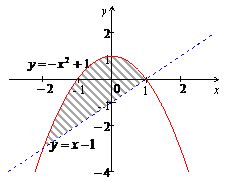
Рис. 6
2. Найдем точки пересечения графиков функции (границы интегрирования). Для этого приравняем функции и решим уравнение по теореме Виета:
-x2+1=x-1
x2+x-2=0
x1=-2; x2=1
3. Вычислим площадь фигуры ограниченной графиками функций, используя геометрический смысл определенного интеграла.
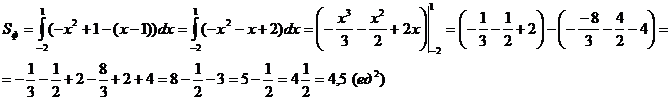
Ответ: Площадь фигуры ограниченной линиями
y=-x2+1, y=x-1 равна 4,5 ед2.
см. также Приложения определённого интеграла.