Интеграл как функция верхнего предела. Формула Ньютона-Лейбница
Рассмотрим функциюТеорема 2.1. Если f(x) интегрируемая на [a,b] функция, то Ф(x) непрерывна на [a,b].
Доказательство. По свойству 9 определенного интеграла (теорема о среднем) имеем
Теорема 2.2. Если f(x) непрерывная на [a,b] функция, то Ф’(x) = f(x) на [a,b].
Доказательство. По свойству 10 определенного интеграла (вторая теорема о среднем), имеем
Таким образом, Ф(x) - одна из первообразных функции f(x) следовательно, Ф(x) = F(x) + C, где F(x) - другая первообразная f(x). Далее, так как Ф(a) = 0, то 0 = F(a) + C, следовательно, C = -F(a) и поэтому Ф(x) = F(x) – F(a). Полагая x=b, получаем формулу Ньютона-Лейбница
Примеры
1. ![]()
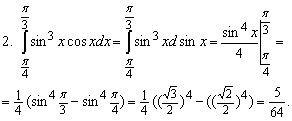
Интегрирование по частям в определённом интеграле
В определенном интеграле сохраняется формула интегрирования по частям. В этом случае она приобретает видПример.
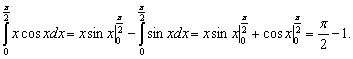
Замена переменных в определённом интеграле
Один из вариантов результатов о замене переменных в определённом интеграле следующий.Теорема 2.3. Пусть f(x)- непрерывна на отрезке [a,b] и
1) φ(α) = a
2) φ(β) = b
3) производная φ’(t) определена всюду на отрезке [α, β]
4)
Тогда
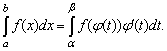
Доказательство. Если F(x) первообразная для f(x)dx то F(φ(t)) первообразная для
Замечание. При отказе от непрерывности функции f(x) в условиях теоремы 2.3 приходится требовать монотонности функции φ(t).
Пример. Вычислить интеграл ![]() Положим
Положим ![]() Тогда dx = 2tdt и поэтому
Тогда dx = 2tdt и поэтому
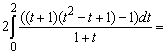
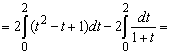
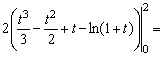
Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.
