Приложения определённого интеграла
Вычисление площадей плоских фигур
Пусть f(x)≥0 для ∀x∈[a,b]. Рассмотрим криволинейную трапецию, ограниченную кривыми y=0, x=a, x=b, y=f(x). Разобьём отрезок [a,b] на части точками a=x0<x1<...<xn=b, выберем внутри каждого элементарного отрезка [xi,i+1] по точке ξi∈[xi,i+1]. Заменим криволинейную трапецию, ограниченную линиями y=0,x=xi, x=xi+1, y=f(x), прямоугольником y=0, x=xi, x=i+1, y=f(ξ). Если f - непрерывная функция, то площадь этого прямоугольника равна f(ξ)·(xi+1-xi)=f(ξ)·Δxi и при достаточно малом Δxi близка площади заменяемой трапеции. Просуммировав, получим, с одной стороны, приближенное значение площади криволинейной трапеции, с другой стороны, интегральную суммуНазовём трапецию простейшей областью, если она ограничена кривыми x = a, x = b, y = f1(x), y = f2(x), и для всех x∈[a,b] выполнено неравенство f1(x) ≤ f2(x). Нетрудно видеть, что для простейшей области
Аналогично, если φ1(y)≤φ2(y) для всех y∈[c,d], то для криволинейной трапеции ограниченной кривыми y=c, y=d, x = φ1(y), x = φ2(y) (простейшей областью второго типа), имеем
В общем случае плоскую область разбивают на простейшие области рассмотренных выше типов.
Примеры
1. Найти площадь фигуры, ограниченной линиями y = x2 и x = y2.
Эти кривые пересекаются в точках A(0,0) и B(1,1). Поэтому 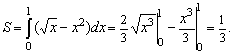
2. Найти площадь фигуры, ограниченной линиями y2 = 2x + 1 и x-y-1=0.
Эти кривые пересекаются в точках A(0,-1) и B(4,3). В данном случае лучше рассматривать простейшую область второго типа. Поэтому
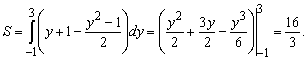
см. также Площадь фигуры, ограниченной линиями: 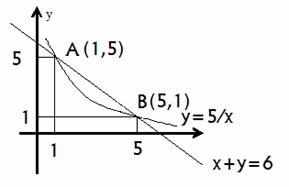
Вычисление объёмов
Пусть область такова, что для ∀x∈[a,b] известна площадь S(x) сечения плоскостью x=const. Тогда, заменяя объём области заключенной между плоскостями x=xi, x=xi+1 на объём цилиндра S(ξ)·Δxi, получаемДля тел, полученных вращением кривой y=f(x) вокруг оси OX, имеем
Примеры
1. Трапеция ограничена кривыми ![]() Вычислить объём тела, полученного вращением этой трапеции вокруг оси OX.
Вычислить объём тела, полученного вращением этой трапеции вокруг оси OX.
Подставляя в формулу, получаем
![]()
см. также Объем фигуры, образованной в результате вращения вокруг оси: 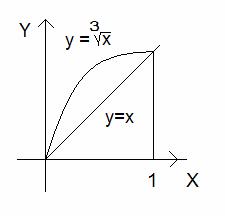
Вычисление длины дуги кривой
Рассмотрим кривую L. Разделим кривую на части точками (xi,yi), i = 1,..,n. Заменим дугу кривой между точками (xi, yi) и (xi+1, yi+1) хордой эти точки соединяющей. Тогда для длины дуги Δli имеемПусть кривая задана параметрически
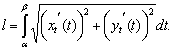 (1)
(1)
Аналогично, для пространственной кривой, заданной параметрически
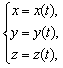 или, что, то же самое, в векторной форме
или, что, то же самое, в векторной форме 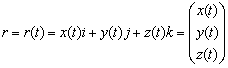 , длина кривой равна
, длина кривой равна
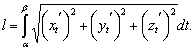 (2)
(2)
Для кривой, заданной явно уравнением y=f(x), формула (1) приобретает вид
Если кривая задана в полярной системе координат, то
Поэтому
Подставляя в формулу для длины кривой, получаем
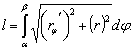 (4)
(4)
Примеры.
1. Найти длину дуги кривой y = ln(x), заключенной между точками ![]() Так как кривая задана явно, то
Так как кривая задана явно, то 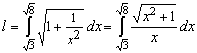 . Делаем замену
. Делаем замену ![]() . Тогда x²=t²-1, 2x·dx=2t·dt и поэтому
. Тогда x²=t²-1, 2x·dx=2t·dt и поэтому ![]()
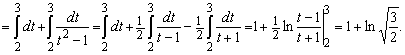
2. Найти длину дуги кривой 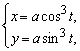 заключенной между точками t1 = 0 и t2 = 2π.
заключенной между точками t1 = 0 и t2 = 2π.
Так как кривая задана параметрически, то x′i=-3·a·cos²(t)·sin(t), y′t=3·a·sin²(t)·cos(t) и поэтому
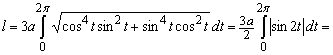
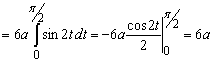 .
.
Вычисление двойных интегралов (криволинейные интегралы). Также рассмотрен пример нахождения центра тяжести однородной плоской фигуры.
Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.
