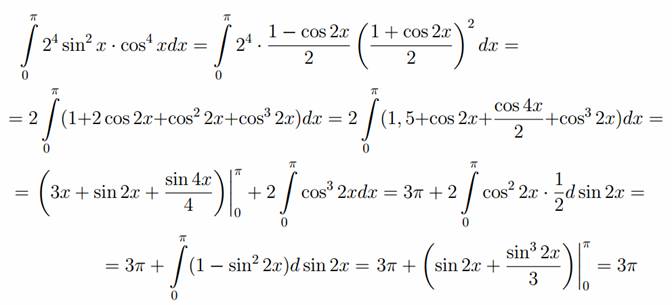Интегрирование тригонометрических функции
Для интегрирования рациональных функций видаR(sin x, cos x) применяют подстановку 
, которая называется универсальной тригонометрической подстановкой. Тогда 
. Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.
- Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x)=t и тогда sin(x)dx = -dt.
- При R(sin(x),-cosx) = - R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
- В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t),
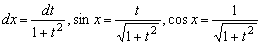, или замену ctg(x)=t, если это удобнее.
Интегрирование функций рационально зависящих от тригонометрических функций
1. Интегралы вида∫sinnxdx, ∫cosnxdx, n>0
a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
2. Интегралы вида
∫tgnxdx, ∫ctgnxdx, где n – целое.
Необходимо использовать формулы
3. Интегралы вида ∫sinnx·cosmx dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x, если n - нечётное либо t=cos x, если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x. Часто бывает удобным применить приём тригонометрической единицы.
5.
∫sin(nx)·cos(mx)dx, ∫cos(mx)·cos(nx)dx, ∫sin(mx)·sin(nx)dx
Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:
- sin α·cos β = ½(sin(α+β)+sin(α-β))
- cos α·cos β = ½(cos(α+β)+cos(α-β))
- sin α·sin β = ½(cos(α-β)-cos(α+β))
Примеры
1. Вычислить интеграл ∫cos4x·sin3xdx.
Делаем замену cos(x)=t. Тогда ∫cos4x·sin3xdx = 
2. Вычислить интеграл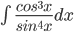 
.
Делая замену sin x=t, получаем
3. Найти интеграл
.
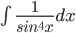Делаем замену tg(x)=t. Подставляя, получаем
, 
и поэтому 
Интегрирование выражений вида R(sinx, cosx)
Пример №1. Вычислить интегралы:
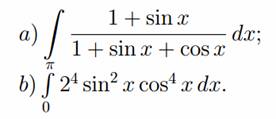
Решение.
а) Интегрирование выражений вида R(sinx, cosx), где R — рациональная функция от sin x и cos x, преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t.
Тогда имеем
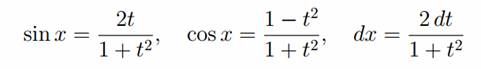
Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида
∫R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:
- Если выполняется равенство
R(-sin x, cos x) = -R(sin x, cos x)dx, то применяется подстановка cos x = t. - Если выполняется равенство
R(sin x, -cos x) = -R(sin x, cos x)dx, то подстановка sin x = t. - Если выполняется равенство
R(-sin x, -cos x) = R(sin x, cos x)dx, то подстановка tgx = t или ctg x = t.
В данном случае для нахождения интеграла
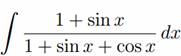
применим универсальную тригонометрическую подстановку tg(x/2) = t.
Тогда
= 
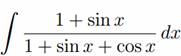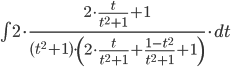
Так как дробь правильная, то, представляем в виде суммы интегралов:
Возвращась к исходной переменной будем иметь
b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫R(sinx, cosx) dx имеет вид ∫sinmx·cosnxdx. В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам: 
В данном случае
