Интегрирование рациональных дробей
Данный онлайн калькулятор служит для вычисления интегралов рациональных дробей вида
.
Пусть подынтегральное выражение есть рациональная дробь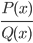 
, где 
и 
- полиномы (многочлены) степеней k и n соответственно. Не умаляя общности, можем считать, что k < n, так как в противном случае всегда можно представить числитель в виде P(x) = Q(x)R(x) + S(x), где R(x) и S(x) - полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома S(x) меньше n. Тогда
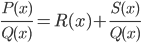, (1.1)
а интеграл от полинома R(x) мы вычислять умеем. Покажем на примере, как можно получить разложение (1.1). Пусть P(x)=x7+3x6+3x5–3x3+4x2+x-2, Q(x)=x3+3x2+x-2. Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор деления столбиком
). Имеем
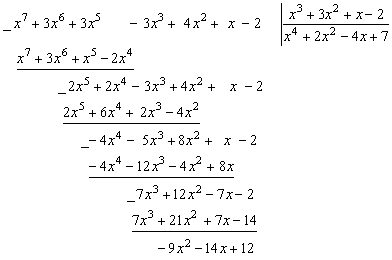
R(x) = x4+2x2–4x+7 и остаток S(x) = 9x2–14x+12 от этого деления.
По основной теореме алгебры любой полином может быть разложен на простейшие множители, то есть представлен в виде
, где xl – корни полинома Q(x) повторенные столько раз, какова их кратность.
Пусть полином Q(x) имеет n различных корней x1, x2,..., xn. Тогда правильная рациональная дробь может быть представлена в виде
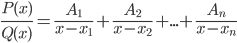, где A1, A2,...,An - числа подлежащие определению. Если xi - корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых 
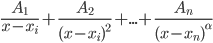. Если xj - комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число xj - тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида 
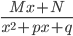, если xj, xj – корни кратности один. Если xj, xj – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид
Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей, из которых 
, 
, 
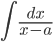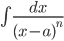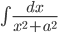являются табличными, 
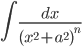может быть найден по рекуррентной формуле, которая получается интегрированием по частям. Интегралы 
, 
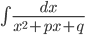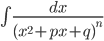в случае, когда знаменатель имеет комплексные корни (дискриминант D=p2-4q<0), сводятся, с помощью выделения полного квадрата, к интегралам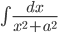 
, 
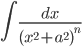заменой 
.
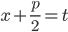Одним из способов нахождения коэффициентов Aj, Mj, Nj в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами Aj, Mj, Nj приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях x (так как полиномы равны, если равны коэффициенты при одинаковых степенях x), получаем систему линейных уравнений для определения этих коэффициентов.
Примеры
1. Найти .
Корни знаменателя – x1 = -2 кратности 1 и x2=1 кратности 2. Поэтому x3 – 3x + 2 = (x+2)(x-1)2 и подынтегральная функция может быть представлена в виде
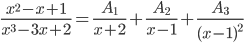
Приводя к общему знаменателю, получаем
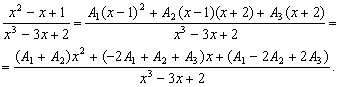
Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем
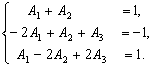
Решая эту систему, находим A1=7/9, A2=2/9, A3=1/3.
Таким образом,
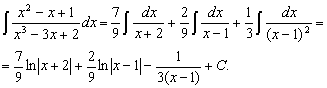
2. Найти
.
Корни знаменателя – x1=2 кратности 1 и два комплексных корня x2,3, = -1±i. Поэтому x3 – 2x – 4 = (x-2)(x2 + 2x+2) и подынтегральная функция может быть представлена в виде
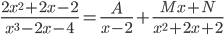
Приводя к общему знаменателю, получаем
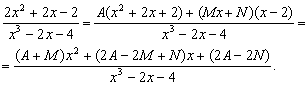
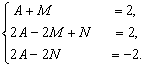
Решая эту систему, находим A=1, M=1, N=2.
Таким образом,
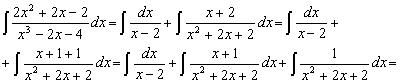
=ln|x-2|+1/2ln(x2+2x+2)+arctg(x+1)+C
Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.
Пример. Найти 
.
Решение. Используем метод разложения на простейшие. Знаменатель имеет действительные корни, причем корень -1 имеет кратность два. Разложим подынтегральную функцию на простейшие слагаемые
2x+1 = A(x-1)2+Bx(x-1) + Dx = (A+B)x2+(-2A-B+D)x+A
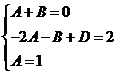→ A=1, B=-1, D=3
Следовательно
