Нахождение производной по ее определению
Пользуясь определением производной, найти производную функции y = sin(αx).Решение.
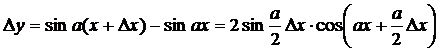 ;
;
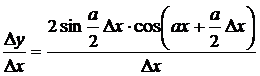
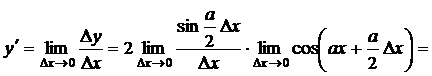
Пример №2. Пользуясь определением, найдите производную функции: f(x) = 3x2 -4x + 5
Решение.
Δf(x) = 3(x+Δx)2 -4(x+Δx) + 5 – (3x2 -4x + 5) = 3(x2+2xΔx + Δx2) -4x-4Δx + 5 – 3x2 +4x – 5 = 6xΔx + 3Δx2-4Δx
![]()
![]()
Ответ: f'(x) = 6x-4
