Оптимальное распределение заказа между фирмами
Предприниматель должен принять решение о приобретении d единиц продукции, которую выпускают две фирмы. Известно, что если он закажет первой фирме х изделий, то ему придется заплатить ейf1(x) = a0 + a1x + a2x2 (руб.),
а при выполнении этого заказа второй фирмой его затраты составят
f2(x) = b0 + b1x + b2x2 (руб.).
Нужно найти оптимальное распределение заказа между фирмами, при котором общие затраты будут минимальными, а также определить максимальный уровень затрат, соответствующий самому неудачному решению предпринимателя.
Исходные значения параметров представлены в таблице:
| d | a0 | a1 | a2 | b0 | b1 | b2 |
| 100 | 25 | 2 | 0.2 | 15 | 6 | 0.3 |
1) составить математическую модель оптимального распределения заказа между фирмами;
2) найти графическим методом распределения заказа с минимальными и максимальными затратами;
3) определить оптимальное распределение заказа методом множителей Лагранжа; дать экономическую интерпретацию множителю Лагранжа.
Решение.
1. Построение математической модели
В данной задаче следует определить
х1 — число изделий, заказанное первой фирме;
х2 — число изделий, заказанное второй фирме.
Эти величины являются переменными модели. Ясно, что они должны принимать неотрицательные значения, т.е. х1 ≥ 0 и х2 ≥ 0; причем их сумма должна равняться общему числу заказанных изделий, т.е. х1 + х2 = 100.
Цель предпринимателя — минимизировать суммарные затраты на выполнение заказа. Так как стоимость х1 изделий, заказанных первой фирме составляет
f1(x1) = 25 + 2 x1+ 0.2x12,
а стоимость х2 изделий, заказанных второй фирме, составляет
f2(x2) = 15 + 6 x2+ 0.3x22,
то суммарные затраты Z на выполнение всего заказа равны
Z = f(x1, x2) = f1(x1) + f2(x2) = 25 + 2 x1+ 0.2x12 + 15 + 6 x2+ 0.3x22 (руб.).
Таким образом, целевая функция (ЦФ) имеет вид:
f(x1, x2) = 40 + 2 x1+ 0.2x12 + 6 x2+ 0.3x22.
Математическая модель задачи может быть записана в таком виде: найти неизвестные значения переменных х1 и х2, доставляющие минимальное значение ЦФ
Z = 40 + 2 x1 + 0.2x12 + 6 x2 + 0.3x22 → min (1)
и удовлетворяющие ограничениям
х1 + х2 = 100, (2)
х1 ≥ 0, х2 ≥ 0. (3)
2. Нахождение графическим методом распределений заказа с минимально и максимально возможными уровнями затрат.
а) Построение ОДР
ОДР состоит из точек плоскости с неотрицательными координатами, которые лежат на прямой, задаваемой уравнением (2). Следовательно, ОДР представляет собой отрезок прямой АВ (см. рис. 1).
б) Построение и анализ линий уровня ЦФ
Приведем ЦФ к более удобному для анализа виду, выделив полные квадраты по каждой ее переменной:
f(х1, х2) = 40 + 2 x1 + 0.2x12 + 6 x2 + 0.3x22 =
0.2(x12 + 10x1 + 25) + 0.3(x22 + 20 x2 + 100) + 5 =
0.2(х1 + 5)2 + 0.3(x2 + 10)2 + 5.
Пусть С — некоторое фиксированное число. Тогда линия уровня функции
f(х1, х2) = С
состоит из всех точек х = (х1, х2) плоскости, координаты которых удовлетворяют уравнению
0.2(х1 + 5)2 + 0.3(x2 + 10)2 + 5 = С
или 0.2(х1 + 5)2 + 0.3(x2 + 10)2 = С – 5. (4)
Так как левая часть этого уравнения неотрицательна при любых значениях х1 и х2, то ясно, что должно выполняться неравенство С ≥ 5, поскольку при С < 5 это уравнение не имеет решений.
Если С = 5, то линия уровня целевой функции содержит единственную точку О = (-5, -10), так как левая часть уравнения (4) равна нулю лишь при х1 = -5 и х2 = ‑10.
При С > 5 линии уровня являются эллипсами с общим центром в точке О, размеры которых увеличиваются с ростом параметра С (см. рис. 1).
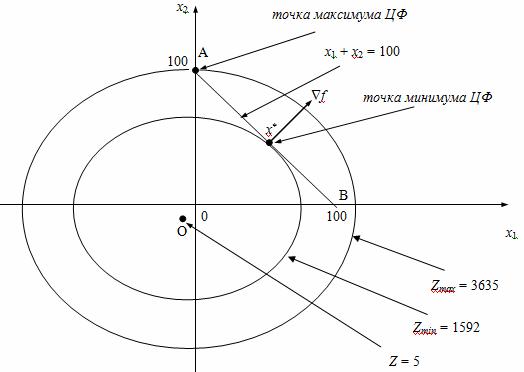
в) Нахождение точки минимума ЦФ
С ростом параметра С линии уровня ЦФ становятся все ближе к ОДР задачи — отрезку АВ. Сначала они не имеют с ним общих точек, но при определенном значении С = Сmin линия уровня коснется этого отрезка в некоторой точке х* = (x1*, x2*). Эта точка соответствует наименьшему значению С, при котором линия уровня имеет общие точки с АВ. Значит, точка х* является решением задачи, так как в ней ЦФ достигает минимума на этом отрезке.
Для определения ее координат воспользуемся следующим фактом. Если прямая
х1 + х2 = 100,
касается в некоторой точке линии уровня ЦФ, задаваемой уравнением
f(х1, х2) = С,
то градиент Ñf =
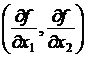, вычисленный в точке касания, перпендикулярен этой прямой. Это означает, что координаты ее вектора нормали прямой, т.е. вектора а = (1, 1), пропорциональны координатам вектора Ñf. Таким образом, выполняется соотношение
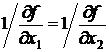или 
.
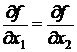Поскольку
= 0.4х1 + 2, а 
= 0.6х2 + 6, то из равенства частных производных получаем, что координаты точки касания удовлетворяют уравнению
0.4·x1+2=0.6·x2+6.
Значит, точку минимума ЦФ можно найти, решив систему уравнений
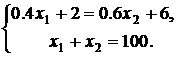
или
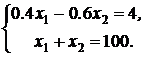(5)
Ее решение: x1*= 64, x2* = 36. Вычислим значение ЦФ в этой точке:
Z* = f(x1*, x2*) = 0.2(64 + 5)2 + 0.3(36 + 10)2 + 5 = 1592 (руб.).
Итак, получено решение задачи (1) – (3): предприниматель должен заказать первой фирме 62 изделия, а второй фирме — 36 изделий. В этом случае его затраты будут минимальными и составят 1592 руб.
г) Нахождение точки максимума ЦФ
При дальнейшем увеличении параметра С линии уровня будут пересекать ОДР в точках, которым соответствуют все возрастающие значения ЦФ. Поэтому последняя точка пересечения является точкой максимума ЦФ на отрезке АВ. Из рис. 1 видно, что в нашей задаче ЦФ достигает максимума в точке А = (0, 100). В этой точке значение ЦФ равно
Zmax = f(0, 100) = 0.2(0 + 5)2 + 0.3(100 + 10)2 + 5 = 3635 (руб.).
Таким образом, самым неудачным решением предпринимателя будет выбор второй фирмы в качестве единственного исполнителя заказа. В этом случае его затраты будут максимальными и составят 3635 руб.
Замечание. Графический анализ показывает, что ЦФ достигает своего максимума в одной из крайних точек отрезка АВ. Поэтому для определения точки максимума проще всего сравнить значения ЦФ в точках А и В. Та точка, в которой это значение больше, будет искомой. Если же значения ЦФ в этих точках равны, то это означает, что обе они являются точками максимума.
3. Нахождение оптимального решения методом множителей Лагранжа
Сначала убедимся в том, что задача (1) – (3) является задачей ВП. Проверим, что ЦФ — выпуклая функция. Для этого вычислим ее гессиан.
Найдем первые частные производные ЦФ:
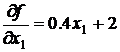и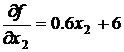 
,
а затем ее вторые частные производные:
;
;
.
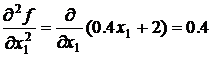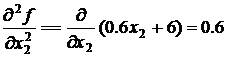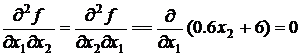Следовательно, гессиан Н функции f имеет следующий вид:
.
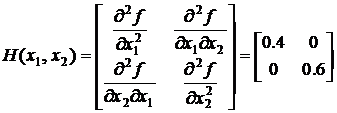Главные миноры первого порядка равны 0.4 и 0.6, а главный минор второго порядка равен
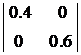= 0.4·0.6 – 0·0 = 0.24.
Значения всех главных миноров не зависят от точки х = (x1, x2) и положительны. Поэтому ЦФ — строго выпуклая функция (см. теорему 1). Так как ограничения модели линейны, то это означает, что задача (1) – (3) является задачей ВП и имеет единственное оптимальное решение.
Чтобы применить метод множителей Лагранжа для решения задачи, следует отбросить условие неотрицательности переменных (3). Тогда исходная задача может быть переформулирована следующим образом: найти неизвестные значения переменных х1 и х2, доставляющие минимальное значение функции
Z = 40 + 2 x1+ 0.2x12> + 6 x2+ 0.3x22> → min (6)
и удовлетворяющие условию
х1 + х2 = 100. (7)
Ясно, что эта задача также является задачей ВП. Отказ от условия (3) приводит к расширению ОДР, так что оптимальное решение задачи (6) – (7) может оказаться недопустимым в исходной задаче (1) – (3). Однако очевидно, что если оптимальное решение задачи (6) – (7) удовлетворяет условию неотрицательности, то это решение будет оптимально и в исходной задаче.
Построим функцию Лагранжа задачи (6) – (7) по формуле (8). Она имеет вид
L(x1, x2, λ) = 40 + 2 x1+ 0.2x12> + 6 x2+ 0.3x22> + λ (100 – х1 – х2). (8)
Найдем частные производные функции L по x1, x2 и λ, а затем приравняем их к нулю. Получим следующую систему уравнений:
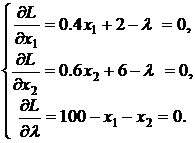(9)
Исключим переменную λ, вычтя из первого уравнения второе. Тогда получим систему уравнений:
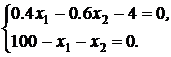(10)
Она фактически совпадает с системой (5) и, значит, имеет такое же решение: x1*=64 и x2*=36. Поскольку задача (6) – (7) является задачей ВП, то из теоремы 6 следует, что вектор х*= (x1*, x2*) = (64, 36) является ее оптимальным решением. Так как найденное решение удовлетворяет условию неотрицательности, то оно будет оптимальным в исходной задаче (1) – (3).
Итак, методом множителей Лагранжа получено оптимальное решение, совпадающее с решением, полученным ранее графическим методом: предприниматель должен распределить заказ между фирмами следующим образом: заказать первой фирме 62 изделия, а второй фирме — 36 изделий. В этом случае его затраты будут минимальными и составят 1592 руб.
Из первого уравнения в системе (9) легко найти оптимальное значение множителя Лагранжа: λ* = 0.4×64 + 2 = 27.6 (руб./ед.).
Множитель Лагранжа λ* имеет такую экономическую интерпретацию: его величина приближенно показывает насколько возрастут минимальные общие затраты Z*(d), если величина заказа d увеличится на единицу, т.е.
λ* ≈ ΔZ*(d) = Z*(d + 1) – Z*(d).
Таким образом, при увеличении заказа от 100 ед. до 101 ед. затраты возрастут примерно на 27.6 руб.
Замечание 1. Точное значение прироста затрат несколько выше: оно равно 27.72 руб. Его можно получить, решив задачу 1 для d = 101. Для этого достаточно найти решение системы, аналогичной (10), в которой второе уравнение имеет следующий вид: 101 – х1 – х2 = 0.
Замечание 2. Решение задачи 1 можно свести к отысканию минимума функции одной переменной на заданном отрезке. Для этого достаточно выразить одну из переменных через другую, используя уравнение (2), а затем подставить полученное выражение в формулу (1), определяющую ЦФ. Однако этот упрощающий прием возможен лишь потому, что ограничение в задаче имеет очень простой вид, и не применим в общем случае. Универсальным способом решения оптимизационных задач с ограничениями типа равенства является метод множителей Лагранжа.