Как найти периметр треугольника
Периметр треугольника равен сумме длин его сторон, т.е. PABC = |AB| + |BC| + |CA|Но как найти периметр треугольника, если треугольник задан через координаты x,y,z? Поясним на примере. Задание. Дано: A(2;1;3); B(2;0;5); C(5;-1;10).
Найти: 1) периметр ABC, с точностью до 0,01; 2) угол ВСА, с точностью до 0,1; 3) площадь ВС, с точностью до 0,01; 4) уравнение прямой В; 5) уравнение плоскости ABC.
Решение.
1) Координаты векторов
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Например, для вектора AB
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 2-2; Y = 0-1; Z = 5-3
AB(0;-1;2)
AC(3;-2;7)
BC(3;-1;5)
2) Модули векторов
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
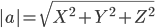
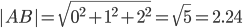
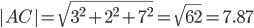
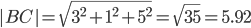
т.е. периметр равен Р = 2.236 + 7.874 + 5.916 =16.026.
3) Угол между ребрами
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле: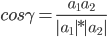
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами AC и BC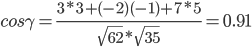
γ = arccos(0.91) = 24.50
7) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле: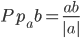
Найдем проекцию вектора AB на вектор AC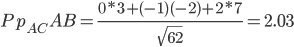
4) Площадь грани
Площадь грани можно найти по формуле: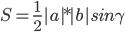
где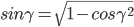
Найдем площадь грани ABC
Найдем угол между ребрами AB и AC: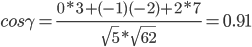
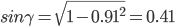
Площадь грани ABC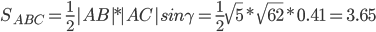
Найдем площадь грани с учётом геометрического смысла векторного произведения: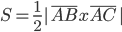
Векторное произведение:
| = |
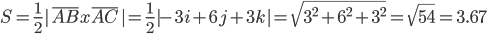
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
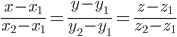
Уравнение прямой AB
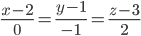
8) Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
| = 0 |
| = 0 |

