Угол между градиентами скалярных полей
Найти угол между градиентами скалярных полей u(x;y;z) и v(x;y;z) в точке М.U(x3+y3+z3), V=x2-y2+z2, M(1;-1;1).
Решение находим с помощью этого калькулятора.
а) Вычислим градиент скалярного поля U(x3+y3+z3) в точке M(1;-1;1). Для этого найдем частные производные
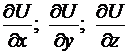и вычислим их значения в точке M(1;-1;1).
; 
; 
.
, 
, 
.
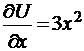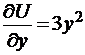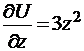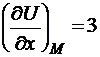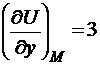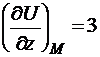Следовательно,
grad U=(3;3;3).
б) Вычислим градиент скалярного поля V=x2-y2+z2 в точке M(1;-1;1). Найдем частные производные
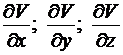и вычислим их значения в точке M(1;-1;1).
; 
; 
.
, 
, 
.
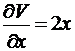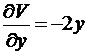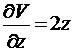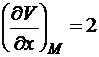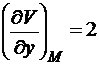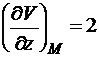Значит, grad V=(2;2;2).
в) Так как градиент – это вектор, то угол между градиентами скалярных полей найдем по формуле: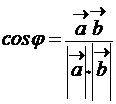 
, т.е. 
.
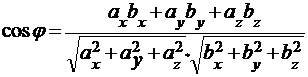Обозначим через φ искомый угол. Тогда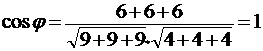 
.
Следовательно, φ=1.
