Решение задачи выпуклого программирования
Рассмотрим задачу выпуклого программирования, в которой ОДР задается системой неравенств:Z = f (x1,…, xn) → max (min), (14)
gi (x1,…, xn) ≤ bi,
. (15)
Выпишем для нее функцию Лагранжа:
L(x, λ) = L(x1,…, xn, λ 1,…, λ m) = f (x1,…, xn) +
λi (bi – gi (x1,…, xn)).
Обозначим I =
— множество индексов ограничений задачи, активных (являющихся равенствами) в некоторой точке 
. Необходимые и достаточные условия того, что эта точка является оптимальным решением задачи (14) – (15) дает следующая теорема.
Теорема 7. Пусть решается задача максимизации (14) – (15), причем функция f вогнутая, функции g1,…, gm выпуклые, все функции непрерывно дифференцируемые и выполнено одно из следующих условий регулярности:
1. существует точка x', такая что gi(x') < bi для всех
(условие Слейтера);
2.
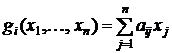для всех 
(линейность ограничений);
3. градиенты ограничений {
} линейно независимы.
В этом случае точка
будет оптимальным решением задачи тогда и только тогда, когда существует вектор 
такой, что
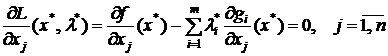; (16)
, ; (17)
, . (18)
Соотношения (16) – (18) называются условиями Куна-Таккера, а вектор
— вектором множителей Лагранжа.
Условие (16) можно записать в векторной форме:
=
.
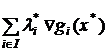Оно означает, что если выполнено любое из условий регулярности, и точка x* является оптимальным решением задачи ВП, то градиент целевой функции представим в виде линейной комбинации градиентов активных ограничений. Отметим, что если решается задача минимизации выпуклой функции, то это условие выглядит несколько иначе:
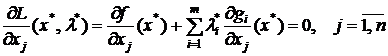. (16¢)
Условие (17) означает, что если множитель Лагранжа положителен, то соответствующее ему ограничение в точке оптимума обязательно должно быть равенством. Если же ограничение не является равенством в точке оптимума, то его множитель Лагранжа равен нулю. Это условие аналогично условию дополняющей нежесткости в задаче ЛП.
В отличие от классической задачи условной оптимизации на множители Лагранжа накладывается условие неотрицательности (18).
Множители Лагранжа допускают интерпретацию, аналогичную интерпретации оптимальных оценок ограничений в задаче ЛП. Так множитель Лагранжа i-го ограничения характеризует величину изменения оптимального значения ЦФ Z* при увеличении правой части этого ограничения на единицу и фиксированных значениях остальных ограничений. А именно, справедлива формула:
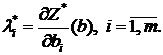(19)
Однако в отличие от задачи ЛП величина
не равна в точности изменению оптимального значения ЦФ при увеличении правой части i-го ограничения на единицу, а дает лишь приближенную оценку этого изменения.
Множество Х называется выпуклым, если для любой пары точек x, y ∈Х и любого числа α∈(0, 1) точка z = αx + (1 – α)y принадлежит этому множеству, то есть, если это множество вместе со своими любыми двумя точками содержит соединяющий их отрезок.
Линии уровня ЦФ рассматриваемой задачи будут эллипсами при выполнения следующих условий: а2 > 0, b2 > 0 и а2 ≠ b2. Если же а2 > 0, b2 > 0, но а2 = b2, то линии уровня представляют собой семейство окружностей, имеющих общий центр О.