Дифференцирование функции, заданной неявно
Пусть дано уравнениеF(x,y)=0, не разрешенное относительно y. Если существует y=f(x) такая, что F[x,f(x)]=0, то говорят, что уравнение F(x,y)=0 задает y как функцию от x неявно. Обычное задание функции y=f(x) называют явным.
При таком способе задания функции производную находим, дифференцируя уравнение F(x,y)=0, считая y функцией от x (по правилу дифференцирования сложной функции).
Правила ввода функции, заданной в неявном виде
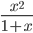≡ x^2/(1+y)
cos2(2x+y) ≡ (cos(2*x+y))^2
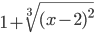≡ 1+(x-y)^(2/3)
Пример 1. Найти производную y’, не решая уравнения: x3 – x2y – x2y4 + 5 = 0 относительно y.
Решение. Так как в правой части уравнения стоит нуль, а производная постоянной равна нулю, то 
.
Применяя почленное дифференцирование, найдем 3x2 – 2xy – x2y’ – 2xy4 – 4x2y3y’ = 0, откуда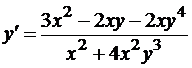 
. 
Пример 2. Найти y’ функции, заданной неявно уравнением y*lnx – x2ey + 1 = 0 (x>0).
Решение.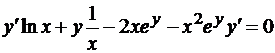 
(производную от ey берем как производную сложной функции). Разрешая уравнение относительно y’ (что не всегда возможно), найдем 
.
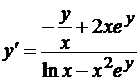Пример 3. Найти производную y’x функции y(x), заданной неявно: x4 + x2y + y3 + 5 = 0.
Решение.
Продифференцируем уравнение по х, рассматривая у как функцию от х, и решим полученное уравнение относительно y’x.
.
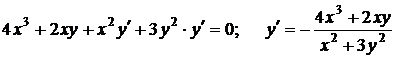