Производная функции, заданная параметрически
Зависимость функции y от аргумента x может осуществляться через посредство третьей переменной t, называемой параметром: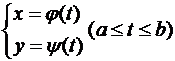
В этом случае говорят, что функция y от x задана параметрически. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.
Предположим, что на некотором промежутке функции x=φ(t) и y=ψ(t) имеют производные, причем φ’(t)≠0. Кроме того, для x=φ(t) существует обратная функция x-1 = t(x) (производная обратной функции равна обратной величине производной прямой функции).
Тогда
y(x)=ψ(t(x)) – сложная функция и ее производная: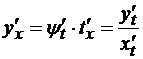 
. Производную тоже запишем в параметрической форме:
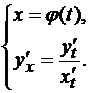
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
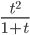≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
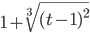≡ 1+(t-1)^(2/3)
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
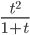≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
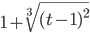≡ 1+(t-1)^(2/3)
Пример 1. Найти производную функции y по x, заданной параметрически: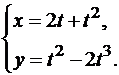 
Решение.
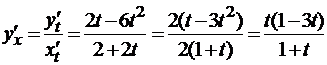.Производные высших порядков
Запишем функцию y’x в параметрической форме: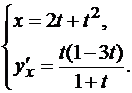
В случае параметрического задания функции
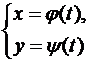первую производную вычисляли по формуле:
(*)
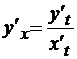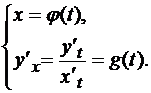
К ней снова применим формулу (*) (при условии, что производные второго порядка существуют):
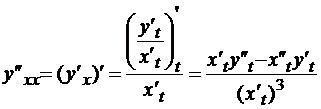.Пример 2. Найти y’’xx функции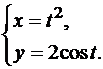 
Решение. Найдем y’x по формуле (*):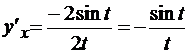 
.
Производную y’x запишем в параметрической форме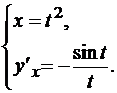 
К этой функции снова применим формулу (*):
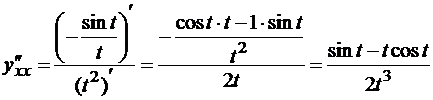.Пример 3. Для функции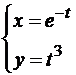 
найти y’’’xxx.
Решение.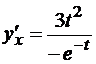 
тогда 
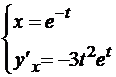и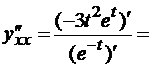 
.
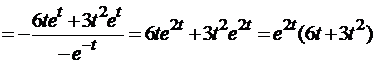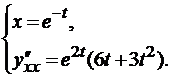
Еще раз применяем формулу (*):
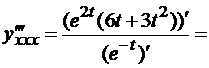
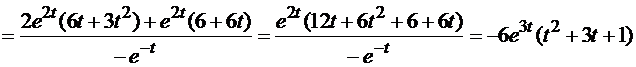.Для функций, заданных неявно, производные высших порядков можно находить тем же способом, что и первую производную, так как производная любого порядка сама является функцией, заданной неявно, если ее не разрешать относительно производной предыдущего порядка.
Пример 7. Найти производную первого и второго порядка функции, заданной параметрически:
.
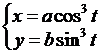Решение.
;
.
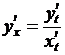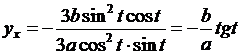Далее будем искать y’’xx по формуле
.
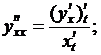Отсюда
.
.
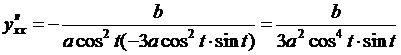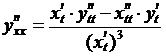