Корреляционный анализ. Подробный пример решения
Целью корреляционного анализа является выявление оценки силы связи между случайными величинами (признаками), которые характеризует некоторый реальный процесс.Задачи корреляционного анализа:
а) Измерение степени связности (тесноты, силы, строгости, интенсивности) двух и более явлений.
б) Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями. Существенные в данном аспекте факторы используют далее в регрессионном анализе.
в) Обнаружение неизвестных причинных связей.
Формы проявления взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи.
Корреляционная связь проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятностных значений независимой переменной. Связь называется корреляционной, если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака.
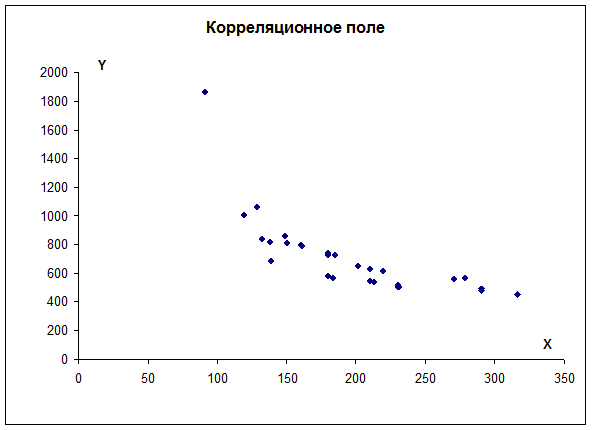
Наглядным изображением корреляционной таблицы служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладываются значения X, по оси ординат – Y, а точками показываются сочетания X и Y. По расположению точек можно судить о наличии связи.
Показатели тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора.
Более совершенным показателем степени тесноты корреляционной связи является линейный коэффициент корреляции. При расчете этого показателя учитываются не только отклонения индивидуальных значений признака от средней, но и сама величина этих отклонений.
Ключевыми вопросами данной темы являются уравнения регрессионной связи между результативным признаком и объясняющей переменной, метод наименьших квадратов для оценки параметров регрессионной модели, анализ качества полученного уравнения регрессии, построение доверительных интервалов прогноза значений результативного признака по уравнению регрессии.
Перейти к онлайн решению своей задачи
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Решение ведем с использованием онлайн-калькулятора Уравнение регрессии
.
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных (см. таблицу расчетов ниже) система уравнений имеет вид:
46a + 17.3101 b = 18.3189
17.3101 a + 7.0687 b = 7.4742
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем b = 1.05, a = 0.0044
Уравнение регрессии: y = 1.05 x + 0.0044
1. Параметры уравнения регрессии.
Выборочные средние.
![]()
![]()
![]()
Выборочные дисперсии:
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.
Коэффициент b = 1.05 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 1.05.
Коэффициент a = 0.0044 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты.
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения Sx приведет к увеличению среднего значения Y на 0.9 среднеквадратичного отклонения Sy.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Дисперсионный анализ.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(yi - ycp)2 = ∑(y(x) - ycp)2 + ∑(y - y(x))2
где
∑(yi - ycp)2 - общая сумма квадратов отклонений;
∑(y(x) - ycp)2 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y - y(x))2 - остаточная сумма квадратов отклонений.
Теоретическое корреляционное отношение для линейной связи равно коэффициенту корреляции rxy.
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:
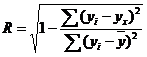
Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R2= 0.89572 = 0.8023
т.е. в 80.23 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 19.77 % изменения Y объясняются факторами, не учтенными в модели.
Посмотреть расчетную таблицу
2. Оценка параметров уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
![]()
![]()
S2y = 0.0034 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
![]()
Sy = 0.0583 - стандартная ошибка оценки (стандартная ошибка регрессии).
Sa - стандартное отклонение случайной величины a.
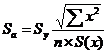
![]()
Sb - стандартное отклонение случайной величины b.
![]()
![]()
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
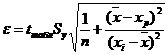
Xp = 0.3763 • 10% = 0.0376
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и Xp = 0.0376
(-0.0123;0.0998)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bxi ± ε)
где
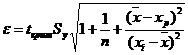
Посмотреть расчетную таблицу
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит (n-m-1;α/2) = (44;0.025) = 2.009
![]()
![]()
Поскольку 13.36 > 2.009, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
![]()
![]()
Поскольку 0.14 < 2.009, то статистическая значимость коэффициента регрессии a не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b - tкрит Sb; b + tкрит Sb)
(1.0467 - 2.009 • 0.0783; 1.0467 + 2.009 • 0.0783)
(0.8893;1.204)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a - tкрит Sa; a + tкрит Sa)
(0.0044 - 2.009 • 0.0307; 0.0044 + 2.009 • 0.0307)
(-0.0573;0.0661)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистика. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
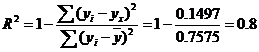
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
![]()
![]()
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=44, Fтабл = 4
Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:
![]()
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения εi с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения εi (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости εi от εi-1
2. Коэффициент автокорреляции.
![]()
Если коэффициент автокорреляции rei < 0.5, то есть основания утверждать, что автокорреляция отсутствует.
3. Критерий Дарбина-Уотсона.
Этот критерий является наиболее известным для обнаружения автокорреляции.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки: условия статистической независимости отклонений между собой. При этом проверяется некоррелированность соседних величин εi.
Посмотреть расчетную таблицу
Для анализа коррелированности отклонений используют статистику Дарбина-Уотсона:
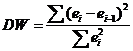
![]()
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n = 46 и количества объясняющих переменных m=1.
Автокорреляция отсутствует, если выполняется следующее условие:
d1 < DW и d2 < DW < 4 - d2.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Поскольку 1.5 < 2.09 < 2.5, то автокорреляция остатков отсутствует.
Для более надежного вывода целесообразно обращаться к табличным значениям.
По таблице Дарбина-Уотсона для n=46 и k=1 (уровень значимости 5%) находим: d1 = 1.50; d2 = 1.59.
Поскольку 1.50 < 2.09 и 1.59 < 2.09 < 4 - 1.59, то автокорреляция остатков отсутствует.
Проверка наличия гетероскедастичности.
1) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X, а по оси ординат либо отклонения ei, либо их квадраты e2i.
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
2) При помощи теста ранговой корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку ei и фактору X. Найдем сумму разности квадратов d2.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
![]()
Посмотреть расчетную таблицу
![]()
Связь между признаком ei и фактором X слабая и обратная
Оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента ранговой корреляции Спирмена
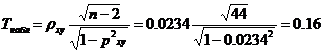
tтабл (n-m-1;α/2) = (44;0.05/2) = 2.009
Поскольку Tнабл < tтабл , то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции. Другими словами, коэффициент ранговой корреляции статистически - не значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал).
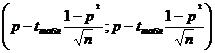
Доверительный интервал для коэффициента ранговой корреляции
r(-0.3194;0.2727)
Проверим гипотезу H0: гетероскедастичность отсутствует.
Поскольку 2.009 > 0.16, то гипотеза об отсутствии гетероскедастичности принимается.
Перейти к онлайн решению своей задачи
Пример 2
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
30a + 5763 b = 21460
5763 a + 1200261 b = 3800360
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем b = -3.46, a = 1379.33
Уравнение регрессии:
y = -3.46 x + 1379.33
2. Расчет параметров уравнения регрессии.
Выборочные средние.
![]()
![]()
![]()
Выборочные дисперсии:
1.1. Коэффициент корреляции
Ковариация.
cov(x,y)=xy-x·y = 126678.67 - 192.17·15.33 = -10736.87
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая и обратная.
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
1.2. Уравнение регрессии (оценка уравнения регрессии).
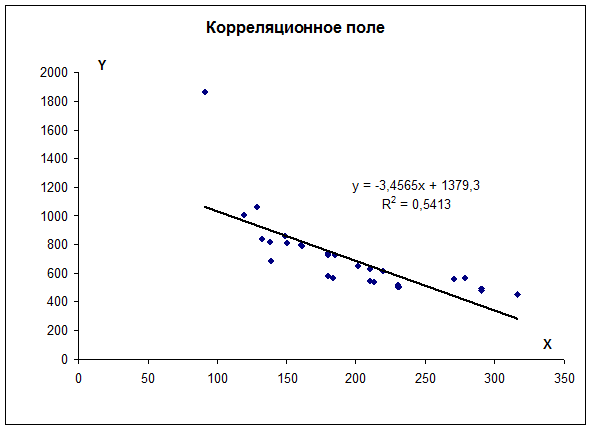
Коэффициент b = -3.46 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y понижается в среднем на -3.46.
Коэффициент a = 1379.33 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь обратная.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты.
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
![]()
![]()
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
![]()
Т.е. увеличение x на величину среднеквадратического отклонения Sx приведет к уменьшению среднего значения Y на 0.74 среднеквадратичного отклонения Sy.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
![]()
![]()
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Дисперсионный анализ.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(yi - ycp)2 = ∑(y(x) - ycp)2 + ∑(y - y(x))2
где
∑(yi - ycp)2 - общая сумма квадратов отклонений;
∑(y(x) - ycp)2 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y - y(x))2 - остаточная сумма квадратов отклонений.
Теоретическое корреляционное отношение для линейной связи равно коэффициенту корреляции rxy.
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:
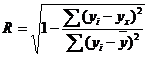
Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R2= -0.742 = 0.5413
т.е. в 54.13 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 45.87 % изменения Y объясняются факторами, не учтенными в модели.
Посмотреть расчетную таблицу
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
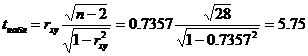
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 - количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
В парной линейной регрессии t2r = t2b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
![]()
S2y = 33699.64 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
![]()
Sy = 183.57 - стандартная ошибка оценки (стандартная ошибка регрессии).
Sa - стандартное отклонение случайной величины a.
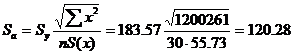
Sb - стандартное отклонение случайной величины b.
![]()
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
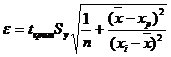
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и Xp = 211
![]()
(1379.33 -3.46*211 ± 72.48)
(577.53;722.49)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bxi ± ε)
где
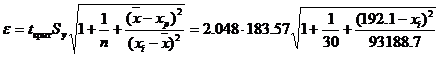
Посмотреть расчетную таблицу
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
![]()
Поскольку 5.75 > 2.048, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
![]()
Поскольку 11.47 > 2.048, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
(-3.4565 - 2.048 • 0.6; -3.4565 + 2.048 • 0.6)
(-4.6881;-2.2249)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a - tкрит Sa; a + tкрит Sa)
(1379.3255 - 2.048 • 120.28; 1379.3255 + 2.048 • 120.28)
(1132.9836;1625.6673)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистика. Критерий Фишера.
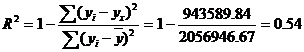
где m – число факторов в модели.
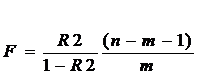
Табличное значение критерия со степенями свободы k1=1 и k2=28, Fтабл = 4.2
Поскольку фактическое значение F > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
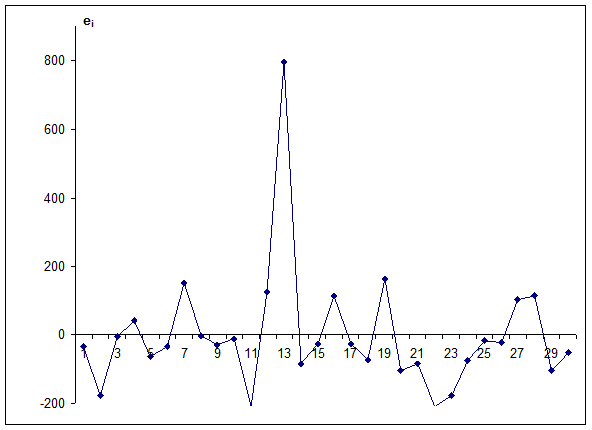
Судя по графику, определенной зависимости не наблюдается.
2. Коэффициент автокорреляции.
Если коэффициент автокорреляции rei < 0.5, то есть основания утверждать, что автокорреляция отсутствует.
Выборочные средние.
Выборочные дисперсии:
Поскольку, rei < 0.1, то можно с уверенностью сказать, что автокорреляция отсутствует.
3. Критерий Дарбина-Уотсона.
Перейти к онлайн решению своей задачи
Список литературы
- Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001, с. 34..89.
- Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. – 2-е изд., испр. – М.: Дело, 1998, с. 17..42.
- Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001, с. 5..48.


