Площадь грани пирамиды
Задание. По координатам пирамиды найти все площади граней.1) Координаты векторов
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Например, для вектора AB
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = -1-3; Y = 6-1; Z = 1-4
AB(-4;5;-3), AC(-4;0;2), AD(-3;3;-5), BC(0;-5;5), BD(1;-2;-2), CD(1;3;-7)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
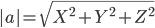
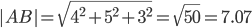
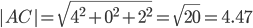
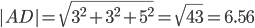
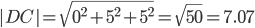
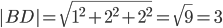
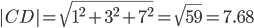
3) Угол между ребрами
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
![]()
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами AB и AC
![]()
4) Площадь грани
Площадь грани можно найти по формуле:
S=½·|a|·|b|·sin γ
![]()
Найдем площадь грани ABC
Найдем угол между ребрами AB и AC:
![]()
![]()
Площадь грани ABC
![]()
Найдем площадь грани ABD
Найдем угол между ребрами AB и AD:
![]()
![]()
Площадь грани ABD
![]()
Найдем площадь грани ACD
Найдем угол между ребрами AC и AD:
![]()
![]()
Площадь грани ACD
![]()
Найдем площадь грани BCD
Найдем угол между ребрами BC и BD:
![]()
![]()
Площадь грани BCD
![]()
5) Объем пирамиды
Объем пирамиды, построенного на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
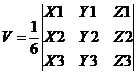
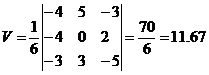
Находим определитель матрицы
∆ = (-4)·(0·(-5)-3·2)-(-4)·(5·(-5)-3·(-3))+(-3)·(5·2-0·(-3)) = -70
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
![]()
Уравнение прямой AB
![]()
Уравнение прямой AC
![]()
Уравнение прямой BC
![]()
Уравнение прямой BD
![]()
Уравнение прямой CD
![]()
8) Уравнение плоскости
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
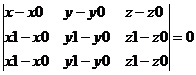
Уравнение плоскости ABC
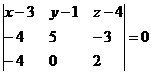
(x-3)(5·2-0·(-3)) - (y-1)((-4)·2-(-4)·(-3)) + (z-4)((-4)·0-(-4)·5) = 10x + 20y + 20z + 130 = 0
Уравнение плоскости ABD
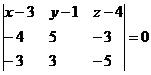
(x-3)(5·(-5)-3·(-3)) - (y-1)((-4)·(-5)-(-3)·(-3)) + (z-4)((-4)·3-(-3)·5) = -16x - 11y + 3z-47 = 0
Уравнение плоскости ACD
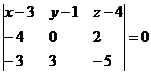
(x-3)(0·(-5)-3·2) - (y-1)((-4)·(-5)-(-3)·2) + (z-4)((-4)·3-(-3)·0) = -6x - 26y - 12z-92 = 0
Уравнение плоскости BCD
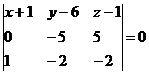
(x+1)((-5)·(-2)-(-2)·5) - (y-6)(0·(-2)-1·5) + (z-1)(0·(-2)-1·(-5)) = 20x + 5y + 5z + 15 = 0
9) Уравнение плоскости, проходящей через точку перпендикулярно вектору
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x0) + m(y- y0) + n(z- z0) = 0
-4(x - (-1)) + 5(y - 1) + (-3)(z - 6) = 0
-4x + 5y -3z + 9 = 0
10) Длина высоты пирамиды, проведенной из вершины A
Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:
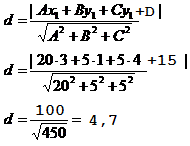
11) Уравнение высоты пирамиды через вершину A
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
![]()
![]()
12) Угол между прямой AB и плоскостью ABC
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле
![]()
![]()
13) Угол между плоскостью ABC и плоскостью ABD
Косинус угла между плоскостью A1x + B1y + C1 + D = 0 и плоскостью A2x + B2y + C2 + D = 0 равен углу между их нормальными векторами N1(A1, B1, C1) и N2(A2, B2, C2):
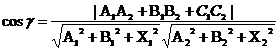
![]()

