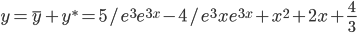Пример решения дифференциального уравнения

Решение находим с помощью сервиса линейные дифференциальные уравнения с постоянными коэффициентами.
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r² -6 r + 9 = 0
D = (-6)² - 4·1·9 = 0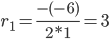


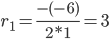
Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e^3x, y₂ = xe^3x
Общее решение однородного уравнения имеет вид: y = C₁·e^3x+C₂·x·e^3x
Найдем частное решение при условии:y(0) = 4/3, y'(0) = 1/27
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 4/3
Находим первую производную:
y' = 3·c1·e^3·x+3·c2·x·e^3·x+c2·e^3·x
Поскольку y'(0) = 3·c1+c2, то получаем второе уравнение:
3·c1+c2 = 1/27
В итоге получаем систему из двух уравнений:
c1 = 4/3
3·c1+c2 = 1/27
т.е.:
c₁ = ⁴/₃, c₂ = ^-107/₂₇
Тогда частное решение при заданных начальных условиях можно записать в виде:

Рассмотрим правую часть:
f(x) = x²-x+3
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e^αx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) - некоторые полиномы
имеет частное решение
y(x) = x^ke^αx(R(x)cos(βx) + S(x)sin(βx))
где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = x²-x+3, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y*=A·x²+B·x+C
Вычисляем производные:
y' = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y' + 9y = (2·A) -6(2·A·x+B) + 9(Ax² + Bx + C) = x²-x+3
или
9·A·x²-12·A·x+2·A+9·B·x-6·B+9·C = x²-x+3
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 1
-12A + 9B = -1
2A -6B + 9C = 3
Решая ее, находим:
A = ¹/₉;B = ¹/₂₇;C = ¹/₃;
Частное решение имеет вид:
y^* = ¹/₉x² + ¹/₂₇x + ¹/₃
Таким образом, общее решение дифференциального уравнения имеет вид:

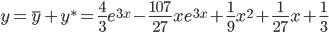
Пример №2. y″ +4y' - 5y = 2·e^x

Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r² +4 r - 5 = 0
D = 4² - 4·1·(-5) = 36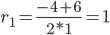


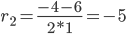
Корни характеристического уравнения:
r₁ = 1
r₂ = -5
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e^x
y₂ = e^-5x
Общее решение однородного уравнения имеет вид: y = C₁·e^3x+C₂·e^-5x
Найдем частное решение при условии:y(0) = 1, y'(0) = -1
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную:
y' = c1·e^x-5·c2·e^-5·x
Поскольку y'(0) = c1-5·c2, то получаем второе уравнение:
c1-5·c2 = -1
В итоге получаем систему из двух уравнений:
c1+c2 = 1
c1-5·c2 = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = ²/₃, c₂ = ¹/₃
Тогда частное решение при заданных начальных условиях можно записать в виде: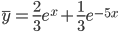

Рассмотрим правую часть:
f(x) = 2·e^x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e^αx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) - некоторые полиномы
имеет частное решение
y(x) = x^ke^αx(R(x)cos(βx) + S(x)sin(βx))
где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = 0, α = 1, β = 0.
Следовательно, число α + βi = 1 + 0i является корнем характеристического уравнения кратности k = 1(r₁).
Уравнение имеет частное решение вида: y*=A·x²+B·x+C
Вычисляем производные: y' = A·e^x(x+1)
y″ = A·e^x(x+2)
которые подставляем в исходное дифференциальное уравнение:
y″ + 4y' -5y = (A·e^x(x+2)) + 4(A·e^x(x+1)) -5(x (Ae^x)) = 2·e^x
или
6·A·e^x = 2·e^x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
6A = 2
Решая ее, находим:
A = ¹/₃;
Частное решение имеет вид:
y^* = x (¹/₃e^x)
Таким образом, общее решение дифференциального уравнения имеет вид:

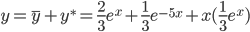
Пример №3. y″ - 4y' + 4y = 2sin(2x), y(0) = 0. y'(0) = -1

Решение:
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r² -4 r + 4 = 0
D = (-4)² - 4·1·4 = 0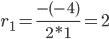


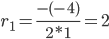
Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e^2x
y₂ = xe^2x
Общее решение однородного уравнения имеет вид: y = C₁·e^2x+C₂·x·e^2x
Найдем частное решение при условии:y(0) = 0, y'(0) = -1
Поскольку y(0) = c1, то получаем первое уравнение:
c1 = 0
Находим первую производную:
y' = 2·c1·e^2·x+2·c2·x·e^2·x+c2·e^2·x
Поскольку y'(0) = 2·c1+c2, то получаем второе уравнение:
2·c1+c2 = -1
В итоге получаем систему из двух уравнений:
c1 = 0
2·c1+c2 = -1
т.е.:
c₁ = 0, c₂ = -1
Тогда частное решение при заданных начальных условиях можно записать в виде:
y =-x·e^2x
Рассмотрим правую часть: f(x) = 2·sin(2·x)
Поиск частного решения.
Здесь P(x) = 0, Q(x) = 2, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y^* = Acos(2x) + Bsin(2x)
Вычисляем производные:
y' = 2·B·cos(2x)-2·A·sin(2x)
y″ = -4(A·cos(2x)+B·sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y″ -4y' + 4y = (-4(A·cos(2x)+B·sin(2x))) -4(2·B·cos(2x)-2·A·sin(2x)) + 4(Acos(2x) + Bsin(2x)) = 2·sin(2·x)
или
8·A·sin(2x)-8·B·cos(2x) = 2·sin(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A = 2
0A -8B = 0
Решая ее, находим:
A = ¹/₄;B = 0;
Частное решение имеет вид:
y^* = ¹/₄cos(2x) + 0sin(2x)
или
y^* = ¹/₄cos(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:

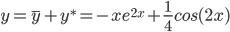
Пример №4. Найти частное решение, общее решение и решение задачи Коши уравнения: y″ - 6y' + 9y = 9x² +6x + 2, y(1) = 1, y'(1) = -1

Решение:
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r² -6 r + 9 = 0
D = (-6)² - 4·1·9 = 0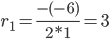


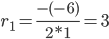
Корни характеристического уравнения:
Корень характеристического уравнения r₁ = 3 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁ = e^3x
y₂ = xe^3x
Общее решение однородного уравнения имеет вид: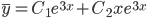

Найдем частное решение при условии:y(1) = 1, y'(1) = -1
Поскольку y(1) = c1·e³+c2·e³, то получаем первое уравнение:
c1·e³+c2·e³ = 1
Находим первую производную:
y' = 3·c1·e^3·x+3·c2·x·e^3·x+c2·e^3·x
Поскольку y'(1) = 3·c1·e³+4·c2·e³, то получаем второе уравнение:
3·c1·e³+4·c2·e³ = -1
В итоге получаем систему из двух уравнений:
c1·e³+c2·e³ = 1
3·c1·e³+4·c2·e³ = -1
которую решаем или методом матриц или методом исключения переменных.
c₁ = 5/e³, c₂ = -4/e³
Тогда частное решение при заданных начальных условиях можно записать в виде: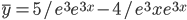

Рассмотрим правую часть:
f(x) = 9·x²+6·x+2
Поиск частного решения.
Здесь P(x) = 9·x²+6·x+2, Q(x) = 0, α = 0, β = 0.
Следовательно, число α + βi = 0 + 0i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида: y*=A·x²+B·x+C
Вычисляем производные:
y' = 2·A·x+B
y″ = 2·A
которые подставляем в исходное дифференциальное уравнение:
y″ -6y' + 9y = (2·A) -6(2·A·x+B) + 9(Ax² + Bx + C) = 9·x²+6·x+2
или
9·A·x²-12·A·x+2·A+9·B·x-6·B+9·C = 9·x²+6·x+2
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
9A = 9
-12A + 9B = 6
2A -6B + 9C = 2
Решая ее, находим:
A = 1;B = 2;C = ⁴/₃;
Частное решение имеет вид:
y^* = x² + 2x + ⁴/₃
Таким образом, общее решение дифференциального уравнения имеет вид:

Перейти к онлайн решению своей задачи