Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид
1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:
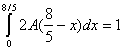

64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то
а) Математическое ожидание.
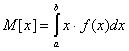



Среднеквадратическое отклонение.
в) Функция распределения F(x) случайной величины X.
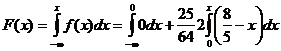


г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.
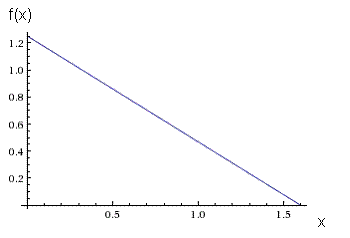
Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.
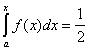
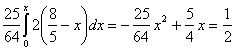
Решая уравнение:
![]()
получаем:
![]()
![]()
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.

е) Вероятность осуществления неравенств ![]() и
и ![]() .
.
