Касательная плоскость и нормаль к поверхности
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0). Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
Вектор
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
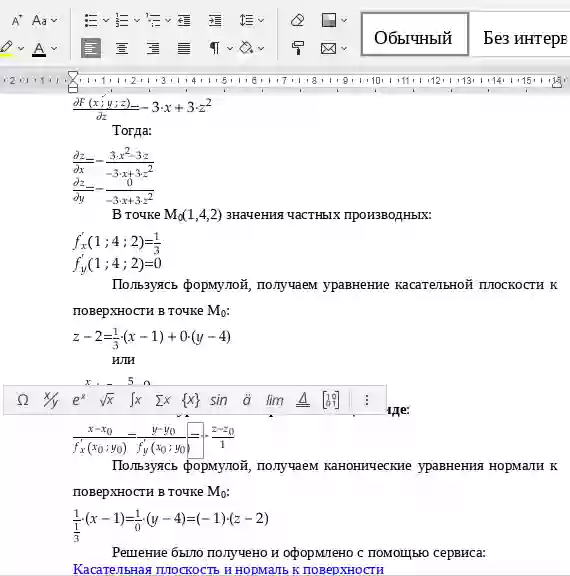
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
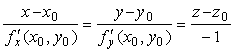
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)
По условию задачи x0 = 0, y0 = 1, тогда z0 = 5
Найдем частные производные функции z = x^3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f'x(x,y) = (x3+5•y)'y = 5
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
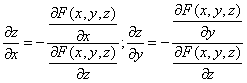
Для нашей функции:
![]()
Тогда:
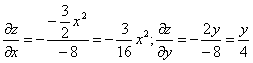
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример. Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
fy’ (x, y) = (y/x + xy – 5x3)’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2)
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0:
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали:
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f'x(x,y) = (x2+3•x•y•+y2)'x = 2•x+3•y3
f'x(x,y) = (x2+3•x•y•+y2)'y = 9•x•y2
В точке М0(1,2) значения частных производных:
f'x(1;2) = 26
f'y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z - 25 = 26(x - 1) + 36(y - 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение