Определённый интеграл
Определение и свойства определённого интеграла
Определение. Пусть функция f(x) определена на отрезке [a,b]. Разобьем отрезок [a,b] на части точками a=x0<x1< ... < xn=b, выберем внутри каждого элементарного отрезка [xi,xi+1] по точке ξi∈[xi, xi+1] и составим сумму
. Предел сумм σn при неограниченном увеличении числа точек разбиения, если этот предел существует, не зависит от способа разбиения, способа выбора точек ξi, при условии, что максимальная длина Δxi=|xi+1-xi| отрезков [xi,xi+1] стремится к нулю, называется определенным интегралом (интегралом Римана) от функции f(x) и обозначается 
Заметим, что если функция f(x) имеет на отрезке [a,b] конечное число точек разрыва первого рода, то для нее существует интеграл Римана.
Отметим некоторые свойства определенного интеграла при условии существования всех используемых ниже интегралов.
1.
2.
3.
4.
5. Если f(x)≥0 и a≤b, то
.
6. Если f(x)≥g(x) и a≤b, то
7.
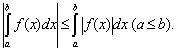
8. Если m≤f(x)≤M и a≤b, то
9.
где μ - некоторое число, m≤μ≤M.
10. Если f(x) непрерывна на [a,b], то существует точка c из [a,b] такая, что
Также рекомендуется изучить сервис решение интегралов онлайн
см. также Интеграл как функция верхнего предела. Формула Ньютона-Лейбница, Несобственные интегралы, Приложения определённого интеграла