Дифференциальное исчисление
Основные понятия и формулыОпределение 1. Производной функции y=f(x) в точке x0 называется предел отношения приращения функции Δf(x) к приращению аргумента Δx, при условии, что приращение аргумента стремится к нулю:
Механический смысл производной.Скорость есть первая производная пути по времени, т.е. v=S'(t).
Геометрический смысл производной. Тангенс угла наклона касательной к графику функции y=f(x) равен первой производной этой функции, вычисленной в точке касания, т.е. tg α=f'(x).
Уравнение касательной к графику функции y=f(x) в точке x0:
y=f(x)+f′(x0)(x-x0)
Уравнение нормали к графику функции y=f(x) в точке x0:
![]()
Правила дифференцирования
(u·v)′ = u′v+uv′(u+v-w)′ = u′+v′+w′
(C·u)′ = C·u′
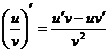
| 1. (C)′=0
2. (x)′=1 3. (xn)′=n·xn-1 4. 5. 6. (ex)′=ex 7. (ax)′=ax·ln(a) 8. (cos x)′= -sin x 9. (sin x)′= cos x 10. |
11. 12. 13. 14. 15. 16. |
Определение 2. Дифференциалом функции y=y(x) называется линейная относительно Δ часть приращения функции. Дифференциал функции находится как произведение производной функции на дифференциал независимой переменной:
dy=y′(x)·dx
Дифференцирование сложной функции
Пусть y=y(u), где u=u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем
y′x=y′u·u′x, или ![]()
Производные высших порядков
Определение 3. Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: y″=[f′(x)]′.Определение 4. Производная n-ого порядка (n-я производная) от функции y=f(x) есть производная от ее (n-1)-й производной: y(n)=[f(n-1)(x)]′.
Пример 9: Найти производную функции ![]()
Решение:![]()
![]()
![]()
![]() +
+
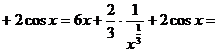
![]()
Пример 10: Найти производную функции y=x²·ln(x)
Решение:
Применим правило дифференцирования (u·v)′ = u′v+uv′
Пример 11: Найти производную функции ![]()
Решение:
Применим правило дифференцирования 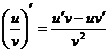
Пример 12: Найти дифференциал функции y=3x²+5
Решение: По определению дифференциал dy=f′·dx
Так как y′=(3x²+5)′=6x, то dy=6x·dx.
Ответ: Дифференциал функции равен dy=6x·dx.
Пример 13: Найти производную сложной функции y=(tg 5x)
Решение:
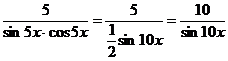
Пример 14: Найти производную функции сложной функции ![]()
Решение:
=
Пример 15: Найти производную второго порядка для функции![]() .
.
Решение:
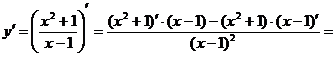
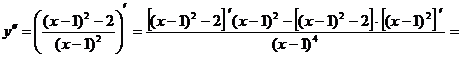
Ответ:
Пример 16: Найти производную второго порядка функции y=ex3 в точке x=1.
Решение: y′=(ex3)′=ex3·(x3)′=ex3·3x2
y″=(3x2·ex3)′ = (3x2)′·ex3+3x2·(ex3)′ = ex3·(6x+9x4) = 3x·ex3(2+3x3)
Найдем y″ при x=1.
y″(1)=3·1·e1·(2+3·1) = 3e·5 = 15e
Ответ: y″(1)=15e
Исследование функций с помощью производной
Определение 1. Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:Определение 2. Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
a. Найти производную функции f′(x).
b. Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
c. Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
d. Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
e. Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Направление выпуклости графика функции. Точки перегиба.
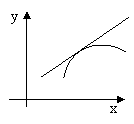
Определение 3: Кривая y=f(x) называется выпуклой вниз на промежутке (a,b), если она лежит выше касательной в любой точке этого промежутка (рис.1).

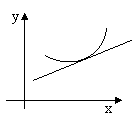
Определение 4: Кривая y=f(x) называется выпуклой вверх на промежутке (a,b), если она лежит ниже касательной в любой точке этого промежутка (рис.2).
Рис.1 Рис. 2
Определение 5. Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба (рис.3).
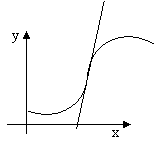
Рис. 3
Правило нахождения точек перегиба графика функции y=f(x)
a. Найти вторую производную f″.
b. Найти точки, в которых вторая производная f″ обращается в нуль или терпит разрыв.
c. Исследовать знак второй производной f″ на каждом промежутке, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
d. Вычислить значения функции в точках перегиба.
Общая схема для построения графиков функций
- Найти область определения функции.
- Исследовать функцию на четность или нечетность.
- Найти точки пересечения графика функций с осями координат.
- Найти асимптоты функции.
- Найти промежутки монотонности и точки экстремума функции.
- Найти промежутки выпуклости и точки перегиба функции.
- По результатам исследования построить график.
Пример 17: Найти промежутки монотонности и экстремумы функции: f(x)=x3-3x2.
Решение: Найдем первую производную функции f′(x)=3x2-6x.
Найдем критические точки по первой производной, решив уравнение 3x2-6x=0.
3x·(x-2)=0
x=0, x=2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | т. max 0 | т. min -4 |
f(2)=23-3·22=-4
Ответ: Функция возрастает при x∈(-∞;0)∪(2;+∞); функция убывает при x∈(0;2); точка минимума функции (2;-4); точка максимума функции (0;0).
Пример 18: Найти промежутки выпуклости и точки перегиба функции f(x)=62-x3.
Решение: Находим f′=12x-32, f″(x)=12-6x.
Найдем критические точки по второй производной, решив уравнение: 12-6x=0, x=2
| x | (-∞;2) | 2 | (2; +∞) |
| f″(x) | + | 0 | - |
| f(x) | ∪ | точка перегиба 16 | ∩ |
Ответ: Функция выпукла вверх при x∈(2;+∞); функция выпукла вниз при x∈(-∞;2); точка перегиба (2;16).
Пример 19. Провести полное исследование функции y=x3-3x и построить ее график.
Решение:
1) Функция определена на всей числовой оси, т. е. ее область определения x∈(-infin;;+∞).
2) Выясним, является ли функция четной или нечетной:
y(-x)=(-x)3-3(-x)=-x3+3x = -(x3-3x) = y(-x)
Отсюда следует, что функция является нечетной, т.е. график симметричен относительно начала координат.
3) Найдем точки пересечения с осями координат:
- с осью ОХ: решим уравнение x3-3x=0
x·(x2-3)=0
![]()
Точки пересечения с осью ОХ ![]()
- с осью ОY: y(0)=03-3·0 = 0
Точка пересечения с осью ОY (0;).
4) Функция непрерывна, асимптот у нее нет.
5) Найдем промежутки монотонности и точки экстремума функции: y′=3x2-3.
Критические точки: 3x2-3 = 0, x2=1, x=±1.
| x | (-∞, -1) | -1 | (-1,1) | 1 | (1,+∞) |
| y′ | + | 0 | - | 0 | + |
| y | т. max 2 | т. min -2 |
y(2)=23-3·2=-2
6) Найдем промежутки выпуклости и точки перегиба функции: y″=6x.
Критические точки: 6x=0, x=0.
| x | (-∞,0) | 0 | (0, +∞) |
| y″ | - | 0 | + |
| y | ∩ | точка перегиба 0 | ∪ |
7) По результатам исследования построим график функции (рис. 4):
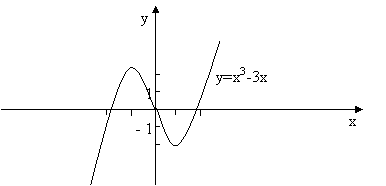
Рис. 4
