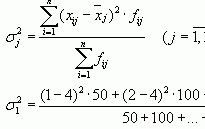Как провести сглаживание ряда экспоненциальным методом
Пример. Построить прогнозный ряд с использованием экспоненциального сглаживания, рассчитать стандартные ошибки. Сравнить прогнозные ряды для а=0,2 и а=0,7 и для скользящего среднего для таблицы 18 представленной в методических указаниях.Решение находим с помощью калькулятора.
Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St - значение экспоненциальной средней в момент t;
St-1 - значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt - значение экспоненциального процесса в момент t;
α - вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 - 0,3). При более высоких значениях (0,3 - 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем среднее арифметическое первых 3 значения ряда.
S0 = (1501 + 2396 + 2328)/3 = 2075
| t | y | St | Формула |
| 1 | 1501 | 1501 | 0.9*1501 + (1 - 0.1)*1501 |
| 2 | 2396 | 2306.5 | 0.9*2396 + (1 - 0.1)*1501 |
| 3 | 2328 | 2325.85 | 0.9*2328 + (1 - 0.1)*2306.5 |
| 4 | 2360 | 2356.59 | 0.9*2360 + (1 - 0.1)*2325.85 |
| 5 | 1738 | 1799.86 | 0.9*1738 + (1 - 0.1)*2356.59 |
| 6 | 1708 | 1717.19 | 0.9*1708 + (1 - 0.1)*1799.86 |
| 7 | 2662 | 2567.52 | 0.9*2662 + (1 - 0.1)*1717.19 |
| 8 | 1944 | 2006.35 | 0.9*1944 + (1 - 0.1)*2567.52 |
| 9 | 963 | 1067.34 | 0.9*963 + (1 - 0.1)*2006.35 |
| 10 | 972 | 981.53 | 0.9*972 + (1 - 0.1)*1067.34 |
| 11 | 1012 | 1008.95 | 0.9*1012 + (1 - 0.1)*981.53 |
| 12 | 926 | 934.3 | 0.9*926 + (1 - 0.1)*1008.95 |
| 13 | 898 | 901.63 | 0.9*898 + (1 - 0.1)*934.3 |
| 14 | 916 | 914.56 | 0.9*916 + (1 - 0.1)*901.63 |
| 15 | 968 | 962.66 | 0.9*968 + (1 - 0.1)*914.56 |
| 16 | 925 | 928.77 | 0.9*925 + (1 - 0.1)*962.66 |
| 17 | 972 | 967.68 | 0.9*972 + (1 - 0.1)*928.77 |
| 18 | 1241 | 1213.67 | 0.9*1241 + (1 - 0.1)*967.68 |
| 19 | 814 | 853.97 | 0.9*814 + (1 - 0.1)*1213.67 |
| 20 | 985 | 971.9 | 0.9*985 + (1 - 0.1)*853.97 |
Аналитическое выравнивание ряда по экспоненте
Экспоненциальное уравнение тренда имеет вид y = a ebt . Оно является частным случаем показательного тренда. Для расчета по МНК уравнение приводят к виду:ln y = ln a + bt
Характеристика параметра k = e экспоненциального тренда выражается в среднем ускорении изменения анализируемого явления от периода (момента) к периоду (моменту) времени.
Пример. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
a0·n+a1∑t=∑y
a1·∑t+a1∑t²=∑y·t
Для наших данных система уравнений имеет вид
18a0+171a1=62.45
171a1+2109a1=542.14
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.11, a1 = 4.47
Уравнение тренда: y = 87.61e-0.11t
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации:
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
Дисперсия
Среднее квадратическое отклонение
Коэффициент детерминации:
т.е. в 70.77 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая
| t | ln(y) | t2 | y2 | t·y | y(t) | (y-y)2 | (y-y(t))2 | (t-tp)2 | (y-y(t)) : y |
| 1 | 4.38 | 1 | 19.2 | 4.38 | 4.37 | 0.83 | 0 | 72.25 | 0.06 |
| 2 | 4.37 | 4 | 19.09 | 8.74 | 4.26 | 0.81 | 0.01 | 56.25 | 0.47 |
| 3 | 4.32 | 9 | 18.64 | 12.95 | 4.16 | 0.72 | 0.03 | 42.25 | 0.7 |
| 4 | 4.25 | 16 | 18.05 | 16.99 | 4.05 | 0.61 | 0.04 | 30.25 | 0.84 |
| 5 | 4.17 | 25 | 17.43 | 20.87 | 3.94 | 0.5 | 0.05 | 20.25 | 0.96 |
| 6 | 4.09 | 36 | 16.76 | 24.57 | 3.84 | 0.39 | 0.07 | 12.25 | 1.04 |
| 7 | 3.66 | 49 | 13.42 | 25.64 | 3.73 | 0.04 | 0 | 6.25 | 0.26 |
| 8 | 3.56 | 64 | 12.64 | 28.44 | 3.63 | 0.01 | 0.01 | 2.25 | 0.26 |
| 9 | 3.4 | 81 | 11.57 | 30.61 | 3.52 | 0 | 0.01 | 0.25 | 0.41 |
| 10 | 3.22 | 100 | 10.36 | 32.19 | 3.42 | 0.06 | 0.04 | 0.25 | 0.64 |
| 11 | 3 | 121 | 8.97 | 32.95 | 3.31 | 0.22 | 0.1 | 2.25 | 0.95 |
| 12 | 2.3 | 144 | 5.3 | 27.63 | 3.21 | 1.36 | 0.82 | 6.25 | 2.08 |
| 13 | 2.56 | 169 | 6.58 | 33.34 | 3.1 | 0.82 | 0.29 | 12.25 | 1.37 |
| 14 | 2.94 | 196 | 8.67 | 41.22 | 2.99 | 0.28 | 0 | 20.25 | 0.15 |
| 15 | 3.37 | 225 | 11.34 | 50.51 | 2.89 | 0.01 | 0.23 | 30.25 | 1.61 |
| 16 | 2.64 | 256 | 6.96 | 42.22 | 2.78 | 0.69 | 0.02 | 42.25 | 0.38 |
| 17 | 3 | 289 | 8.97 | 50.93 | 2.68 | 0.22 | 0.1 | 56.25 | 0.95 |
| 18 | 3.22 | 324 | 10.36 | 57.94 | 2.57 | 0.06 | 0.42 | 72.25 | 2.08 |
| 171 | 62.45 | 2109 | 224.33 | 542.14 | 62.45 | 7.63 | 2.23 | 484.5 | 15.21 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 0.0165
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (16;0.05) = 1.746
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 10
87.61 e-0.11*10 - 1.746*0.65 ; 87.61 e-0.11*10 + 1.746*0.65
(29.82;31.12)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество
наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого
показателя; Tтабл - табличное значение критерия Стьюдента для
уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 19: y(19) = 87.61 e-0.11*19 = 11.78
K1 = 1.3
11.78 - 1.3 = 10.48 ; 11.78 + 1.3 = 13.08
Интервальный прогноз:
t = 19: (10.48;13.08)
2) F-статистика. Критерий Фишера.
Fkp = 4.45
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | ei= y-y(x) | e2 | (ei- ei-1)2 |
| 4.38 | 4.37 | 0.01 | 0 | 0 |
| 4.37 | 4.26 | 0.11 | 0.01 | 0.01 |
| 4.32 | 4.16 | 0.16 | 0.03 | 0 |
| 4.25 | 4.05 | 0.2 | 0.04 | 0 |
| 4.17 | 3.94 | 0.23 | 0.05 | 0 |
| 4.09 | 3.84 | 0.26 | 0.07 | 0 |
| 3.66 | 3.73 | -0.07 | 0 | 0.11 |
| 3.56 | 3.63 | -0.07 | 0.01 | 0 |
| 3.4 | 3.52 | -0.12 | 0.01 | 0 |
| 3.22 | 3.42 | -0.2 | 0.04 | 0.01 |
| 3 | 3.31 | -0.32 | 0.1 | 0.01 |
| 2.3 | 3.21 | -0.9 | 0.82 | 0.35 |
| 2.56 | 3.1 | -0.54 | 0.29 | 0.14 |
| 2.94 | 2.99 | -0.05 | 0 | 0.24 |
| 3.37 | 2.89 | 0.48 | 0.23 | 0.28 |
| 2.64 | 2.78 | -0.14 | 0.02 | 0.39 |
| 3 | 2.68 | 0.32 | 0.1 | 0.21 |
| 3.22 | 2.57 | 0.65 | 0.42 | 0.11 |
| 0 | 0 | 0 | 2.23 | 1.85 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Для более надежного вывода целесообразно обращаться к табличным значениям.
d1 < DW и d2 < DW < 4 - d2.