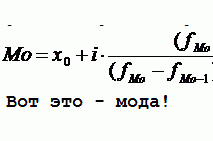Метод наименьших квадратов
Метод наименьших квадратов позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных y(x) минимальна: ∑(y - yx)2 → minСистема нормальных уравнений для линейной регрессии:
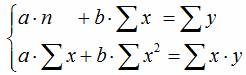
Пример №1. Функция задана таблицей
| X | -2 | -1 | 0 | 1 | 2 |
| Y | 3.1 | 1.7 | 0.9 | 0.7 | 1.05 |
Применяя метод наименьших квадратов, приблизить ее многочленами 1-й и 2-й степени. Для каждого приближения определить величину среднеквадратичной погрешности, построить график.
Рекомендации к решению. На первом шаге в калькуляторе необходимо выбрать Вид сглаживани: по прямой
. Чтобы получить приближение 2-й степени необходимо выбрать Вид сглаживани: по параболе
.
Пример №2. По 10 парам наблюдений получены следующие результаты: ∑xi = 100; ∑yi = 200; ∑xiyi = 21000; ∑yi2 = 12000; ∑yi2 = 45000. По МНК оцените коэффициенты линейных уравнений регрессии Y на X и X на Y. Оцените коэффициент корреляции и детерминации. Проинтерпретируйте результаты.
Решение.
Уравнение регрессии X на Y: y = a + bx
Найдем средние значения.
x– = 100/10 = 10; y– = 200/10 = 20; xy– = 21000/10 = 2100;
b = (2100-10×20)/(12000/10-102) = 1.727
a = 20 – 1.727×10 = 2.727
y = 2.727 + 1.727x
Уравнение регрессии Y на X: x = a + by = (y-2.727)/1.727 = 0,579x – 1.579
Дисперсии
σx2 = 12000/10 – 102 = 1100
σy2 = 45000/10 – 202 = 4100
Среднеквадратические отклонения
σx = (1100)1/2 = 33.17
σy = (4100)1/2 = 64.03
Коэффициент корреляции rxy = b σx/σy = 1.727×33.17/64.03 = 0.895
Коэффициент детерминации: R2 = 0,8952 = 0.8. Следовательно, в 80% случаев изменения х приводят к изменению y. Другими словами, точность подбора уравнения регрессии - высокая.
Пример №3. В задачах результаты измерений величин x и y даются таблицей. Предполагая, что между переменными x и y существует линейная функциональная зависимость y = ax + b, найти, пользуясь способом наименьших квадратов эту функцию. Вычислить с помощью полученной формулы приближенные значения y при x = 2.5 и x=6.
Сглаживание ряда методом наименьших квадратов
Задание.1. Постройте прогноз численности наличного населения города Б на 2010-2011 гг., используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните полученные результаты, сделайте вывод.
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
9a0 + 45a1 = 524.9
45a0 + 285a1 = 2610.4
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.24, a1 = 59.5
Уравнение тренда:
y = -0.24 t + 59.5
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -0.24 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -0.24.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
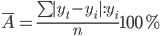
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
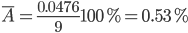
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
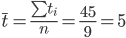
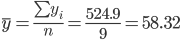
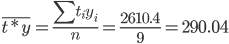
Дисперсия
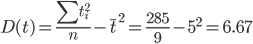
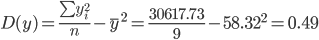
Среднеквадратическое отклонение
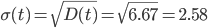
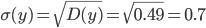
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
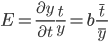
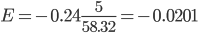
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами - влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
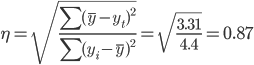
где (y-yt)² = 4.4-1.08 = 3.31
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
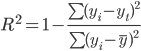
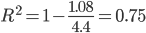
т.е. в 75.39% случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда - высокая.
| t | y | y(t) | (y-ycp)2 | (y-y(t))2 | (t-tp)2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
Определим среднеквадратическую ошибку прогнозируемого показателя.
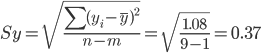
m = 1 - количество влияющих факторов в уравнении тренда.
Uy=yn+L±K
где
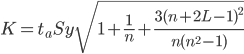
L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (7;0.025) = 2.365
Точечный прогноз, t = 10: y(10) = -0.24*10 + 59.5 = 57.15
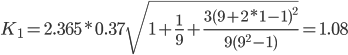
57.15 - 1.08 = 56.07 ; 57.15 + 1.08 = 58.23
Интервальный прогноз:
t = 10: (56.07;58.23)
Точечный прогноз, t = 11: y(11) = -0.24*11 + 59.5 = 56.91
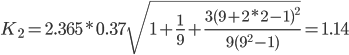
56.91 - 1.14 = 55.77 ; 56.91 + 1.14 = 58.05
Интервальный прогноз:
t = 11: (55.77;58.05)
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | - | - |
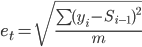
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St - значение экспоненциальной средней в момент t;
St-1 - значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt - значение экспоненциального процесса в момент t;
α - вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 - 0,3). При более высоких значениях (0,3 - 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 - 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 - 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 - 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 - 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 - 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 - 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 - 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 - 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 - 0.1)*56.9 + 0.1*57.54 |
Методы прогнозирования под названием "сглаживание" учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 - α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
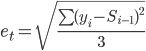
где i = (t - 2, t)
Пример. Методом наименьших квадратов найти функции вида y=ax+b, y=ax²+bx+c, аппроксимирующие экспериментальную функцию y=f(x). В обоих случаях найти суммы квадратов невязок ∑bi². В декартовой системе координат построить экспериментальные точки и графики найденных функций y=ax+b,y=ax^2+bx+c.
Пример №5
Пример №6
Пример №3. Функция y=y(x) задана таблицей своих значений:
x: -2 -1 0 1 2
y: -0,8 -1,6 -1,3 0,4 3,2
Применяя метод наименьших квадратов, приблизить функцию многочленами 1-ой и 2-ой степеней. Для каждого приближения определить величину среднеквадратичной погрешности. Построить точечный график функции и графики многочленов.
Решение. Функция многочлена 2-ой степени имеет вид y = ax2+ bx + c.
1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a0n + a1∑x + a2∑x2= ∑y
a0∑x + a1∑x2+ a2∑x3= ∑yx
a0∑x2+ a1∑x3+ a2∑x4= ∑yx2
| x | y | x2 | y2 | x y | x3 | x4 | x2y |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -2 | -0.8 | 4 | 0.64 | 1.6 | -8 | 16 | -3.2 |
| -1 | -1.6 | 1 | 2.56 | 1.6 | -1 | 1 | -1.6 |
| 0 | -1.3 | 0 | 1.69 | 0 | 0 | 0 | 0 |
| 1 | 0.4 | 1 | 0.16 | 0.4 | 1 | 1 | 0.4 |
| 2 | 3.2 | 4 | 10.24 | 6.4 | 8 | 16 | 12.8 |
| 0 | -0.1 | 10 | 15.29 | 10 | 0 | 34 | 8.4 |
6a0+ 0a1+ 10a2= -0.1
0a0+ 10a1+ 0a2= 10
10a0+ 0a1+ 34a2= 8.4
Получаем a0= 0.494, a1= 1, a2= -0.84
Уравнение: y = 0.494x2+x-0.84
