Решение типовых задач по статистике

Задача I
Джон пользовался мобильным телефоном 30 дней. Ежедневное количество звонков

3	4	2	1	1
3	9	1	4	2
6	4	9	13	15
2	5	5	2	7
3	0	1	2	7
1	8	6	9	4

а) составьте распределение частот из 6 групп.
б) вычислите распределение относительных частот.
Решение.
а) Составим распределение частот из 6 групп, используя этот калькулятор. Ширина интервала составит:

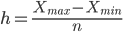
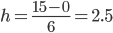
Xmax - максимальное значение группировочного признака в совокупности.
Xmin - минимальное значение группировочного признака.
Определим границы группы.

Номер группы	Нижняя граница	Верхняя граница
1	0	2.5
2	2.5	5
3	5	7.5
4	7.5	10
5	10	12.5
6	12.5	15

Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.

0	0 - 2.5	1
1	0 - 2.5	2
1	0 - 2.5	3
1	0 - 2.5	4
1	0 - 2.5	5
1	0 - 2.5	6
2	0 - 2.5	7
2	0 - 2.5	8
2	0 - 2.5	9
2	0 - 2.5	10
2	0 - 2.5	11
3	2.5 - 5	1
3	2.5 - 5	2
3	2.5 - 5	3
4	2.5 - 5	4
4	2.5 - 5	5
4	2.5 - 5	6
4	2.5 - 5	7
5	2.5 - 5	8
5	2.5 - 5	9
6	5 - 7.5	1
6	5 - 7.5	2
7	5 - 7.5	3
7	5 - 7.5	4
8	7.5 - 10	1
9	7.5 - 10	2
9	7.5 - 10	3
9	7.5 - 10	4
13	12.5 - 15	1
15	12.5 - 15	2

Результаты группировки оформим в виде таблицы:

Группы	№ совокупности	Частота fi
0 - 2.5	1,2,3,4,5,6,7,8,9,10,11	11
2.5 - 5	12,13,14,15,16,17,18,19,20	9
5 - 7.5	21,22,23,24	4
7.5 - 10	25,26,27,28	4
10 - 12.5	0	0
12.5 - 15	29,30	2

Таблица для расчета показателей.

Группы	x_i	Кол-во, f_i	x_i * f_i	Накопленная частота, S	\|x - x_ср\|*f	(x - x_ср)²*f	Частота, f_i/n
0 - 2.5	1.25	11	13.75	11	35.75	116.19	0.37
2.5 - 5	3.75	9	33.75	20	6.75	5.06	0.3
5 - 7.5	6.25	4	25	24	7	12.25	0.13
7.5 - 10	8.75	4	35	28	17	72.25	0.13
10 - 12.5	11.25	0	0	28	0	0	0
12.5 - 15	13.75	2	27.5	30	18.5	171.13	0.0667
		30	135		85	376.88	1

б) Вычислим распределение относительных частот, используя сервис дискретной случайной величины

x	1.25	3.75	6.25	8.75	11.25	13.75
p	0.37	0.3	0.13	0.13	0	0.0667

Математическое ожидание находим по формуле m = ∑x_ip_i.
Математическое ожидание M[X].
M[x] = 1.25*0.37 + 3.75*0.3 + 6.25*0.13 + 8.75*0.13 + 11.25*0 + 13.75*0.0667 = 4.455
Дисперсию находим по формуле d = ∑x²_ip_i - M[x]².
Дисперсия D[X].
D[X] = 1.25²*0.37 + 3.75²*0.3 + 6.25²*0.13 + 8.75²*0.13 + 11.25²*0 + 13.75²*0.0667 - 4.455² = 12.595
Среднее квадратическое отклонение σ(x).

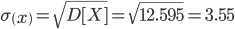
Функция распределения F(X).
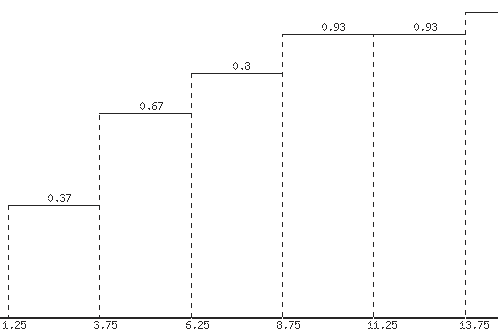
F(x≤1.25) = 0
F(1.25< x ≤3.75) = 0.37
F(3.75< x ≤6.25) = 0.3 + 0.37 = 0.67
F(6.25< x ≤8.75) = 0.13 + 0.67 = 0.8
F(8.75< x ≤11.25) = 0.13 + 0.8 = 0.93
F(11.25< x ≤13.75) = 0 + 0.93 = 0.93
F(x>13.75) = 1

Функция распределения F(X)

Многоугольник распределения

Задача 2
Вычислите среднее медиану и моду для следующего набора данных:
84, 82, 90, 77, 75, 77, 82, 86, 82.

Решение
Видео решение

Решение. Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.

75
77
77
82
82
82
84
86
90

Таблица для расчета показателей.

x_i	Кол-во, f_i	x_i * f_i	Накопленная частота, S	\|x - x_ср\|*f	(x - x_ср)²*f	Частота, f_i/n
75	1	75	1	6.67	44.44	0.11
77	2	154	3	9.33	43.56	0.22
82	3	246	6	1	0.33	0.33
84	1	84	7	2.33	5.44	0.11
86	1	86	8	4.33	18.78	0.11
90	1	90	9	8.33	69.44	0.11
	9	735		32	182	1

Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная

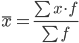
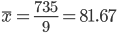
Мода
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
Максимальное значение повторений при x = 82 (f = 3). Следовательно, мода равна 82
Медиана
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим x_i, при котором накопленная частота S будет больше ∑f/2 = 5. Это значение x_i = 82. Таким образом, медиана равна 82

Задача 3
Одна компания подсчитала количество своих сотрудников, распределив их по уровню, соответствующему количеству лет работы на компанию.

Кол-во лет работы	Кол-во сотрудников
1	5
2	7
3	10
4	8
5	12
6	3

Каково среднее количество лет работы в данной компании.
Методические рекомендации к решению. Задачу необходимо решать через сервис Показатели вариации. В исходных условиях задать: Вариационный ряд.

Задача 4.
Распределение студентов одного из факультетов по возрасту (лет) характеризуется следующими данными:

Возраст студентов, Лет	17	18	18	20	21	22	23	24	Всего
Число студентов	20	80	90	110	130	170	90	60	750

Вычислите по этим данным:
а) размах вариации;
б) среднее линейное отклонение;
в) дисперсию;
г) среднее квадратическое отклонение;
д) коэффициент вариации.
Сделайте вывод об однородности совокупности.
Методические рекомендации к решению. Задача решается с помощью калькулятора Показатели вариации. В исходных условиях задать: Вариационный ряд.
Задача 5
В порядке механической выборки обследован возраст 100 студентов вуза из общего числа 2000 чел.

Возраст, Лет	17	18	19	20	21	22	23
Число студентов	11	13	18	23	17	10	8

Установите:
а) средний возраст студента вуза по выборке;
б) величину ошибки при определении возраста студентов на основе выборки;
в) вероятные пределы колебания возраста для всех студентов при вероятности 0,997.

Решение
Видео решение

Решение. Таблица для расчета показателей.

x_i	Кол-во, f_i	x_i * f_i	Накопленная частота, S	\|x - x_ср\|*f	(x - x_ср)²*f	Частота, f_i/n
17	11	187	11	31.24	88.72	0.11
18	13	234	24	23.92	44.01	0.13
19	18	342	42	15.12	12.7	0.18
20	23	460	65	3.68	0.59	0.23
21	17	357	82	19.72	22.88	0.17
22	10	220	92	21.6	46.66	0.1
23	8	184	100	25.28	79.88	0.08
	100	1984		140.56	295.44	1

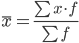
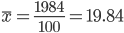
Мода
Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
Максимальное значение повторений при x = 20 (f = 23). Следовательно, мода равна 20
Медиана
Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим x_i, при котором накопленная частота S будет больше ∑f/2 = 51. Это значение x_i = 20. Таким образом, медиана равна 20
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = X_max - X_min
R = 23 - 17 = 6
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

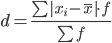
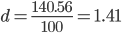
Каждое значение ряда отличается от другого в среднем на 1.41
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

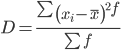
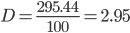
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.

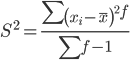
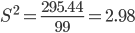
Среднее квадратическое отклонение.

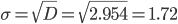
Каждое значение ряда отличается от среднего значения 19.84 в среднем на 1.72
Оценка среднеквадратического отклонения.

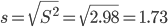
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

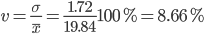
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая.
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.

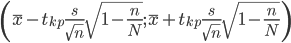
или

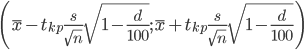
где d - процент выборки.
В этом случае 2Ф(t_kp) = γ
Ф(t_kp) = γ/2 = 0.997/2 = 0.4985
По таблице функции Лапласа найдем, при каком t_kp значение Ф(t_kp) = 0.4985
t_kp(γ) = (0.4985) = 2.96

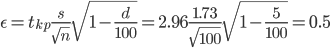
(19.84 - 0.5;19.84 + 0.5) = (19.34;20.34)
С вероятностью 0.997 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.

Задача 6.
Есть ли статистически значимая связь между удовлетворенностью перспективами должностного и профессионального роста в зависимости от пола респондента.

пол	удовлетворенность		Σ
пол	доволен	не доволен	Σ
Ж	4	8	12
М	12	6	18
Σ	16	14	30

Решаем задачу с помощью калькулятора Коэффициент контингенции. Пример решения.

см. также примеры решения задач по статистике.

Новые калькуляторы

Решение типовых задач по статистике

Правила ввода данных