Аналитическая геометрия
Даны вершины A1, A2, A3, A4. По координатам вершин пирамиды найти:- Длины ребер A1A2 и A1A3, угол между ребрами A1A2 и A1A3;
- Площадь грани A1A2A3, объем пирамиды A1A2A3A4;
- Уравнение прямой, проходящей через точки A1 и A2, уравнение прямых A2A3 и A1A3;
- Уравнение плоскостей A1A2A3 и A1A2A4, угол между плоскостями A1A2A3 и A1A2A4;
- Записать вектора AB(A1A2) и AC (A1A3 в системе орт), проекцию вектора AD на вектор AB.
- Уравнение плоскости, проходящей через точку перпендикулярно вектору, уравнение прямой, проходящей через данную точку перпендикулярно данной плоскости
- Длину высоты пирамиды, проведенной из вершины, уравнение высоты пирамиды через вершину, расстояние от точки до плоскости.
Инструкция. Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее. см. также по координатам треугольника найти.
Пример №1. В пирамиде SABC: треугольник ABC - основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x2 - x1; Y = y2 - y1; Z = z2 - z1
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2).
Длину вектора находим по формуле:
![]()
Угол между векторами a1 и a2 находят с помощью формулы:
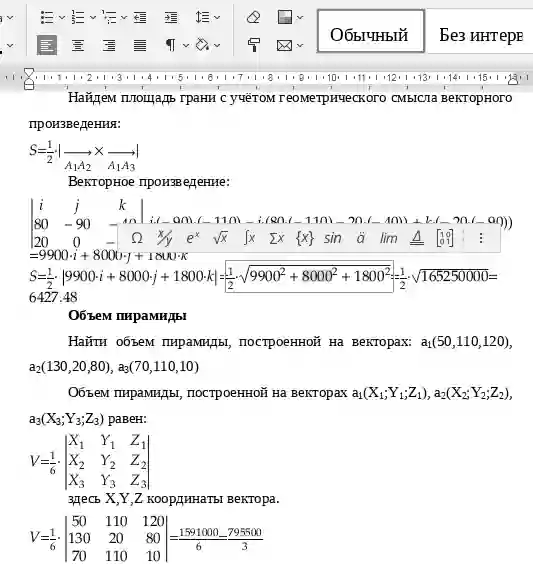
Найдем площадь грани с учётом геометрического смысла векторного произведения:
Векторное произведение:
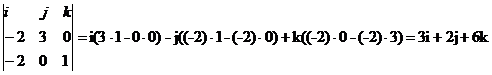
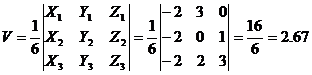
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнением:
Уравнение плоскости, при условии, что точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, представляется уравнением:
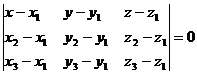
Уравнение плоскости ABC запишем как:
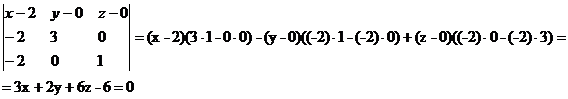
3x + 2y + 6z-6 = 0
Длина высоты пирамиды, проведенной из вершины D, выражается формулой:
Пример №2. В тетраэдре ABCD вычислить:
- объем тетраэдра ABCD;
- высоту тетраэдра, опущенную из вершины D на грань ABC.
Пример №3. Даны координаты четырех точек в пространстве. Используя векторное и смешанное произведения векторов, найти площадь треугольника ABC и объем тетраэдра ABCD. Сделать схематический рисунок.