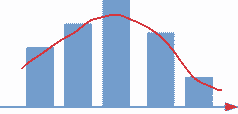
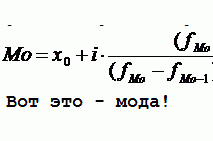Прогнозирование объема товарооборота на основе тренда
Цель: спрогнозировать объем товарооборота на основе данных таблицы.Задачи исследования:
- определить параметры тренда
- спрогнозировать объем товарооборота
- оценить погрешность прогноза.
Решение находим с помощью калькулятора.
Линейное уравнение тренда имеет вид y = at + b
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
Для наших данных система уравнений имеет вид:
45a0 + 1035a1 = 4141.61
1035a0 + 31395a1 = 93922.83
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.18, a1 = 96.08
Уравнение тренда
y = -0.18*t + 96.08
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
![]()
![]()
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
![]()
![]()
![]()
Дисперсия
![]()
![]()
Среднеквадратическое отклонение
![]()
![]()
Коэффициент эластичности
![]()
![]()
Коэффициент эластичности меньше 1. Следовательно, с изменение периода мало влияет на изменение товарооборота.
Коэффициент детерминации
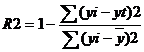
![]()
т.е. в 0.22 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда – низкая. Полученное уравнение тренда не желательно использовать для прогнозирования.
2. Анализ точности определения оценок параметров уравнения тренда.
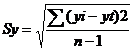
Анализ точности определения оценок параметров уравнения тренда
![]()
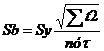
![]()
![]()
S a = 0.5684
Доверительные интервалы для зависимой переменной
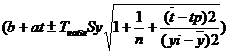
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (43;0.025) = 2.009
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 25.
(96.08 -0.18*25 - 2.009*100.61 ; 96.08 -0.18*25 - 2.009*100.61)
(-8.92;192.29)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
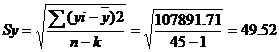
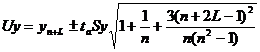
где L - период упреждения; уn+L - точечный прогноз по модели на (n + L)-й момент времени; n - количество наблюдений во временном ряду; Sy - стандартная ошибка прогнозируемого показателя; Tтабл - табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n-2.
Проверим качество полученного уравнения тренда.
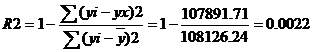
![]()
Fkp = 4
Поскольку F < Fkp, то коэффициент детерминации статистически не значим. Это еще раз подтверждает, что данное уравнение тренда не желательно использовать для прогноза товарооборота. Необходимо выбрать другую модель: по параболе, экспоненциальную, степенную или другую.
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1
Критерий Дарбина-Уотсона.
Этот критерий является наиболее известным для обнаружения автокорреляции.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки: условия статистической независимости отклонений между собой. При этом проверяется некоррелированность соседних величин ei.
| y | y(x) | ei= y-y(x) | e2 | (ei- ei-1)2 |
| 115 | 95.9 | 19.1 | 364.69 | 0 |
| 85 | 95.73 | -10.73 | 115.07 | 889.48 |
| 69 | 95.55 | -26.55 | 704.98 | 250.41 |
| 57 | 95.38 | -38.38 | 1472.69 | 139.81 |
| 184.6 | 95.2 | 89.4 | 7992.38 | 16326.65 |
| 56 | 95.02 | -39.02 | 1522.88 | 16492.78 |
| 85 | 94.85 | -9.85 | 96.99 | 851.23 |
| 265 | 94.67 | 170.33 | 29011.44 | 32463.31 |
| 60.65 | 94.5 | -33.85 | 1145.6 | 41687.11 |
| 130 | 94.32 | 35.68 | 1272.99 | 4833.83 |
| 46 | 94.15 | -48.15 | 2317.96 | 7026.5 |
| 115 | 93.97 | 21.03 | 442.29 | 4785.29 |
| 70.96 | 93.79 | -22.83 | 521.37 | 1924.07 |
| 39.5 | 93.62 | -54.12 | 2928.74 | 978.7 |
| 78.9 | 93.44 | -14.54 | 211.47 | 1566.24 |
| 60 | 93.27 | -33.27 | 1106.64 | 350.6 |
| 100 | 93.09 | 6.91 | 47.74 | 1614.09 |
| 51 | 92.91 | -41.91 | 1756.84 | 2383.8 |
| 157 | 92.74 | 64.26 | 4129.49 | 11273.3 |
| 123.5 | 92.56 | 30.94 | 957.09 | 1110.5 |
| 55.2 | 92.39 | -37.19 | 1382.9 | 4640.91 |
| 95.5 | 92.21 | 3.29 | 10.81 | 1638.29 |
| 57.6 | 92.04 | -34.44 | 1185.82 | 1423.12 |
| 64.5 | 91.86 | -27.36 | 748.57 | 50.07 |
| 92 | 91.68 | 0.32 | 0.0997 | 765.95 |
| 100 | 91.51 | 8.49 | 72.11 | 66.84 |
| 81 | 91.33 | -10.33 | 106.76 | 354.35 |
| 65 | 91.16 | -26.16 | 684.18 | 250.41 |
| 110 | 90.98 | 19.02 | 361.72 | 2040.85 |
| 42.1 | 90.81 | -48.71 | 2372.21 | 4586.57 |
| 135 | 90.63 | 44.37 | 1968.74 | 8663.1 |
| 39.6 | 90.45 | -50.85 | 2586.1 | 9067.65 |
| 57 | 90.28 | -33.28 | 1107.42 | 308.91 |
| 80 | 90.1 | -10.1 | 102.05 | 537.12 |
| 61 | 89.93 | -28.93 | 836.73 | 354.35 |
| 69.6 | 89.75 | -20.15 | 406.05 | 77.01 |
| 250 | 89.57 | 160.43 | 25736.24 | 32607.61 |
| 64.5 | 89.4 | -24.9 | 619.96 | 34345.07 |
| 125 | 89.22 | 35.78 | 1279.98 | 3681.55 |
| 152.3 | 89.05 | 63.25 | 4000.88 | 754.92 |
| 110 | 88.87 | 21.13 | 446.41 | 1774.45 |
| 40.6 | 88.7 | -48.1 | 2313.21 | 4791.99 |
| 95 | 88.52 | 6.48 | 41.99 | 2978.52 |
| 98 | 88.34 | 9.66 | 93.23 | 10.09 |
| 52 | 88.17 | -36.17 | 1308.16 | 2099.86 |
| 107891.72 | 264817.26 |
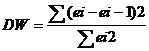
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n = 45 и количества объясняющих переменных m=1.
Автокорреляция отсутствует, если выполняется следующее условие:
d1 < DW и d2 < DW < 4 - d2.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 < DW < 2.5. Поскольку 1.5 < 2.45 < 2.5, то автокорреляция остатков отсутствует.
Для более надежного вывода целесообразно обращаться к табличным значениям.
По таблице Дарбина-Уотсона для n=45 и k=1 (уровень значимости 5%) находим: d1 = 1.48; d2 = 1.57.
Поскольку 1.48 < 2.45 и 1.57 < 2.45 < 4 - 1.57, то автокорреляция остатков присутствует.
Проверка наличия гетероскедастичности.
1) Методом графического анализа остатков.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X, а по оси ординат либо отклонения ei, либо их квадраты e2i.
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
2) При помощи теста ранговой корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку ei и фактору t. Найдем сумму разности квадратов d2.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
| X | ei | ранг X, dx | ранг ei, dy | (dx- dy)2 |
| 1 | -19.1 | 1 | 12 | 121 |
| 2 | 10.73 | 2 | 23 | 441 |
| 3 | 26.55 | 3 | 29 | 676 |
| 4 | 38.38 | 4 | 38 | 1156 |
| 5 | -89.4 | 5 | 3 | 4 |
| 6 | 39.02 | 6 | 39 | 1089 |
| 7 | 9.85 | 7 | 20 | 169 |
| 8 | -170.33 | 8 | 1 | 49 |
| 9 | 33.85 | 9 | 34 | 625 |
| 10 | -35.68 | 10 | 8 | 4 |
| 11 | 48.15 | 11 | 42 | 961 |
| 12 | -21.03 | 12 | 11 | 1 |
| 13 | 22.83 | 13 | 26 | 169 |
| 14 | 54.12 | 14 | 45 | 961 |
| 15 | 14.54 | 15 | 24 | 81 |
| 16 | 33.27 | 16 | 32 | 256 |
| 17 | -6.91 | 17 | 16 | 1 |
| 18 | 41.91 | 18 | 40 | 484 |
| 19 | -64.26 | 19 | 4 | 225 |
| 20 | -30.94 | 20 | 9 | 121 |
| 21 | 37.19 | 21 | 37 | 256 |
| 22 | -3.29 | 22 | 18 | 16 |
| 23 | 34.44 | 23 | 35 | 144 |
| 24 | 27.36 | 24 | 30 | 36 |
| 25 | -0.32 | 25 | 19 | 36 |
| 26 | -8.49 | 26 | 15 | 121 |
| 27 | 10.33 | 27 | 22 | 25 |
| 28 | 26.16 | 28 | 28 | 0 |
| 29 | -19.02 | 29 | 13 | 256 |
| 30 | 48.71 | 30 | 43 | 169 |
| 31 | -44.37 | 31 | 6 | 625 |
| 32 | 50.85 | 32 | 44 | 144 |
| 33 | 33.28 | 33 | 33 | 0 |
| 34 | 10.1 | 34 | 21 | 169 |
| 35 | 28.93 | 35 | 31 | 16 |
| 36 | 20.15 | 36 | 25 | 121 |
| 37 | -160.43 | 37 | 2 | 1225 |
| 38 | 24.9 | 38 | 27 | 121 |
| 39 | -35.78 | 39 | 7 | 1024 |
| 40 | -63.25 | 40 | 5 | 1225 |
| 41 | -21.13 | 41 | 10 | 961 |
| 42 | 48.1 | 42 | 41 | 1 |
| 43 | -6.48 | 43 | 17 | 676 |
| 44 | -9.66 | 44 | 14 | 900 |
| 45 | 36.17 | 45 | 36 | 81 |
| 15942 |
![]()
Связь между признаком Y фактором X слабая и обратная
Оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента ранговой корреляции Спирмена
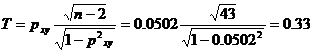
По таблице Стьюдента находим tтабл:
tтабл (n-m-1;α/2) = (43;0.05/2) = 2.009
Поскольку Tнабл < tтабл , то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции. Другими словами, коэффициент ранговой корреляции статистически - не значим.
Поскольку 2.009 > 0.33, то гипотеза об отсутствии гетероскедастичности принимается.