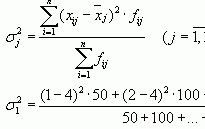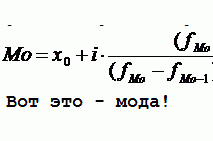Критерий серий, основанный на медиане выборки
Присутствие тренда не всегда четко прослеживается во временном ряду. В этих случаях прежде, чем перейти к определению тенденции и выделению тренда, нужно выяснить, существует ли вообще тенденция в исследуемом процессе.Основные подходы к решению этой задачи основаны на статистической проверке гипотез. Критерии выявления компонент ряда основаны на проверке гипотезы о случайности ряда.
Наиболее часто используемые на практике критерии проверки
наличия-отсутствиятренда: критерий серий, основанный на медиане выборки и метод Фостера-Стюарта.
Назначение сервиса. Онлайн калькулятор используется для определения тенденции в ряду с помощью критерия серий, основанного на медиане выборки.
Инструкция. Укажите количество данных (количество строк). Полученное решение сохраняется в файле Word.
Алгоритм метода
Критерий серий, основанный на медиане выборки, реализуется в виде следующей последовательности шагов:- 1) Из исходного ряда yt длиной n образуется ранжированный (вариационный) ряд yt
- Определяется медиана этого вариационного ряда Me. В случае нечетного значения n (n=2m+1) Me=ym+1, в противном случае Me=(ym+ym+1)/2.
- Образуется последовательность δi из плюсов и минусов по следующему правилу:
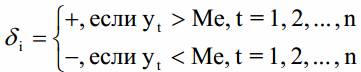
Если значение yt равно медиане, то это значение пропускается. - Подсчитывается v(n) - число серий в совокупности δi, где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или один минус тоже будет считаться серией. Определяется t(n) - протяженность самой длинной серии.
- Проверка гипотезы основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий - слишком маленьким. Поэтому для того, чтобы не была отвергнута гипотеза о случайности исходного ряда (об отсутствии систематической составляющей) должны выполняться следующие неравенства (для 5% уровня значимости uкр = 1.96):
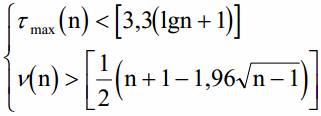
Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии тренда отвергается.
Квадратные скобки в правой части неравенства означают целую часть числа.
Пример. По данным любого статистического ежегодника органов госстатистики или по данным периодических изданий постройте интервальный, абсолютный, равноотстоящий ряд динамики (12-15 уровней). По данным ряда:
- проведите аналитическое выравнивание по прямой методом реального и условного времени.
- проведите аналитическое выравнивание по параболе методом реального и условного времени.
- Проверьте правильность выбранного уравнения тренда на основе: средней квадратической ошибки; дисперсионного метода анализа; критерия серий, основанного на медиане выборки, критерия «восходящих» и «нисходящих» серий